10. 인공 신경망
인공 신경망
뇌에 있는 생물학적 뉴런의 네트워크에서 영감을 받은 머신러닝 모델
- 하지만 생물학적 뉴런(신경 세포)에서 점점 멀어지고 있음
- 딥러닝의 핵심이며, 복잡한 대규모 머신러닝 문제를 다루는 데 적합
- 구글 이미지와 같이 수백만 개의 이미지 분류
- 애플의 시리처럼 음성 인식 서비스 성능 향상
- 유튜브처럼 수억 명의 사용자에게 비디오 추천
- 알파고와 같이 수백만 개의 기보를 익히고 자기 자신과 게임하며 학습
10. 1 생물학적 뉴런에서 인공 뉴런까지
10. 1. 1 생물학적 뉴런
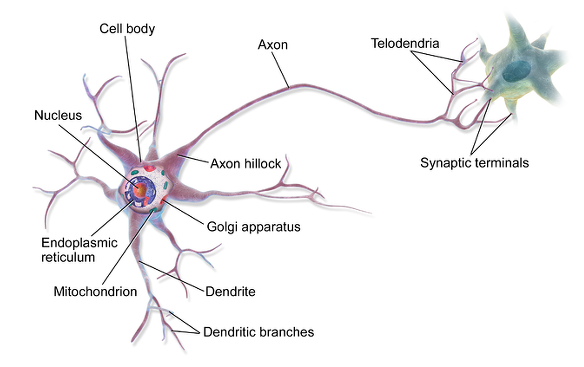
- 생물학적 뉴런은 활동 전위(AP) 또는 간단히 신호라고 부르는 짧은 전기 자극을 만듦
- 각각의 뉴런은 수상돌기(Dendrite)를 통해 다른 뉴런에서 신호를 받아서 축삭돌기(Axon)를 통해 다른 뉴런으로 신호를 보냄
- 시냅스(Synapse)는 뉴런과 뉴런을 연결하는 역할을 함
- 전달된 신호는 시냅스가 신경전달물질 이라는 화학적 신호를 발생하게 함
10. 1. 2 뉴런을 사용한 논리 연산
매컬러와 피츠가 생물학적 뉴런에서 착안하여 제안한 매우 단순한 신경망 모델 - 인공 뉴런
- 이 모델은 하나 이상의 이진 입력과 이진 출력을 가짐
- 이런 간단한 모델로 인공 뉴런의 네트워크를 만들어 어떤 논리 명제도 계산할 수 있음
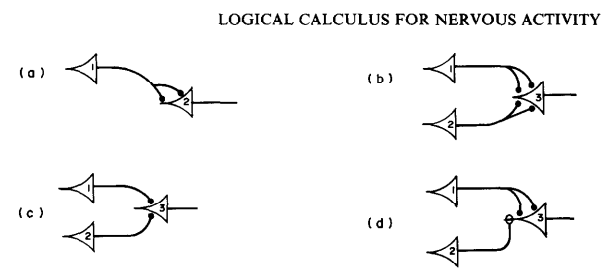
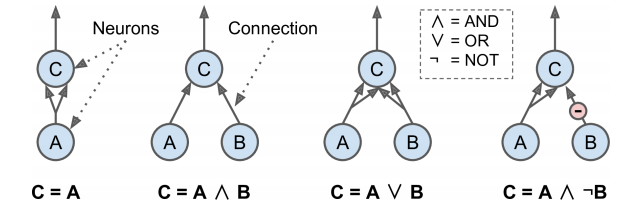
- 1. 첫 번째 네트워크
- 항등 함수
- 뉴런 A가 활성화되면 뉴런 C도 활성화됨
- 뉴런 A가 꺼지면 뉴런 C도 비활성화
- 2. 두 번째 네트워크
- 논리곱 연산
- 뉴런 A, B 모두 활성돠될 때만 뉴런 C가 활성화됨
- 입력 신호 하나만으로 뉴런 C를 활성화하지 못함
- 3. 세 번째 네트워크
- 논리합 연산
- 뉴런 A, B 중 하나가 (혹은 둘 다) 활성화되면 뉴런 C가 활성화됨
- 4. 네 번째 네트워크
- 어떤 입력이 뉴런의 활성화를 억제할 수 있음
- 뉴런 A가 활성화되고 뉴련 B가 비활성화될 때 뉴런 C가 활성화 됨
- 뉴런 A가 항상 활성화되어 있다면 이 네트워크는 논리 부정 연산이 됨
복잡한 논리 표현식을 계산하기 위해 이런 식으로 네트워크들을 연결할 수 있음
10. 1. 3 퍼셉트론
가장 간단한 인공 신경망 구조 중 하나로, 1957년 프랑크 로젠블라트가 제안
퍼셉트론은 TLU(threshold logic unit) 또는 LTU(linear threshold unit)라고 불리는 다른 형태의 인공 뉴런을 기반으로 함
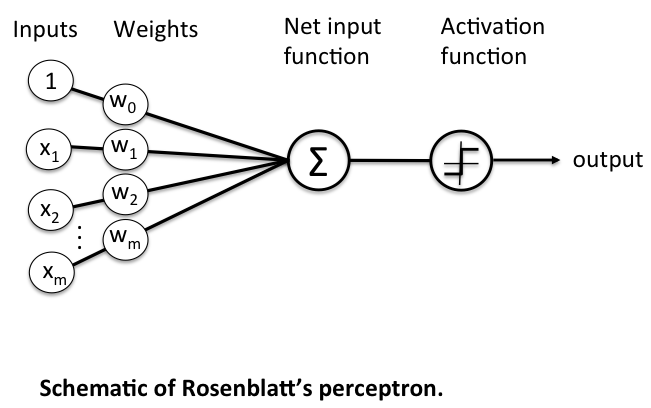
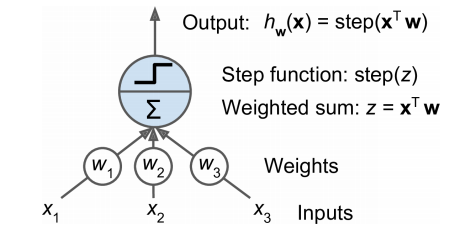
- 입력과 출력이 (이진이 아닌) 어떤 숫자이고, 각각의 입력 연결을 가중치과 연관되어 있음
- TLU는 입력의 가중치 합을 계산(z = w1x1+w2x2+...+x^Tw)한 뒤 계산된 합에 계단 함수를 적용하여 결과를 출력 => hx(x) = step(z), (z = x^Tw)
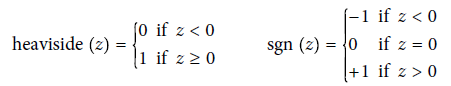
- 퍼셉트론에서 가장 널리 사용되는 계단 함수는 헤비사이드 계단 함수 (이따금 부호 함수를 사용하기도 함)
하나의 TLU는 간단한 선형 이진 분류 문제에 사용할 수 있음
- 입력의 선형 조합을 계산해 그 결과가 임계값을 넘으면 양성 클래스, 아니면 음성 클래스를 출력
(로지스틱 회귀나 선형 SVM 분류기처럼)
- EX) 하나의 TLU를 이용해 꽃잎 길이와 너비를 기반으로 붓꽃의 품종을 분류할 수 있음
- 이 경우 TLU를 훈련한다는 것은 최적의 w0, w1, w2를 찾는다는 뜻
퍼셉트론은 층이 하나뿐인 TLU로 구성됨
- 퍼셉트론을 하나의 TLU를 가진 작은 네트워크를 의미하는 용도로 사용하곤 함
- 각 TLU는 모든 입력에 연결되어 있음
-
완전 연결 층 (밀집 층) : 한 층에 있는 모든 뉴런이 이전 층의 모든 뉴런과 연결되어 있는 경우
-
퍼셉트론의 입력은 입력 뉴런이라 불리는 특별한 통과 뉴런에 주입됨
-
이 뉴런은 어떤 입력이 주입되는 그냥 출력으로 통과시킴
-
-
입력층은 모두 입력 뉴런으로 구성 됨
- 여기세 편향 특성이 더해짐 (x0=1)
- 전형적으로 이 편향 특성은 항상 1을 출력하는 특별한 종류의 뉴런인 편향 뉴런으로 표현됨
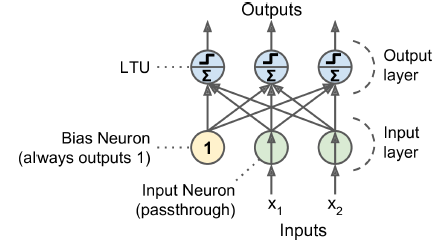
- 입력 두 개와 출력 세 개로 구성된 퍼셉트론
- 이 퍼셉트론은 샘플을 세 개의 다른 이진 클래스로 동시에 분류할 수 있으므로 다중 레이블 분류기
h w,b(x) = Φ(XW + b)
완전 연결 층의 출력 계산
- 위 식으로 한 번에 여러 샘플에 대해 인공 뉴런 층의 출력을 효율적으로 계산할 수 있음
-
X는 입력 특성의 행렬 (행은 샘플, 열은 특성)
-
가중치 행렬 W는 편향 뉴런을 제외한 모든 연결 가중치를 포함함
-
이 행렬의 행은 입력 뉴런에 해당
-
열은 출력층에 있는 인공 뉴런에 해당
-
-
편향 벡터 b는 편향 뉴런과 인공 뉴런 사이의 모든 연결 가중치를 포함 (인공 뉴런마다 하나의 편향 값이 있음
-
Φ는 활성화 함수 (인공 뉴런이 TLU일 경우 이 함수는 계단 함수)
퍼셉트론의 훈련
프랑크 로젠블라트가 제안한 퍼셉트론의 훈련 알고리즘은 헤브의 규칙에서 영감 받음
- 생물학적 뉴런이 다른 뉴런을 활성화시킬 때 이 두 뉴런의 연결이 강해진다는 아이디어에서 출발
=> "서로 활성화되는 세포가 서로 연결된다"
=> 두 뉴런이 동시에 활성화될 때마다 이들 사이의 연결 가중치가 증가하는 경향이 있음
- 이 규칙은 후에 헤브의 규칙(헤브 학습)으로 알려짐
- 퍼셉트론은 네트워크가 예측할 때 만드는 오차를 반영하도록 조금 변형된 규칙을 사용하여 훈련
- 퍼셉트론 학습 규칙은 오차가 감소되도록 연결을 강화시킴
=> 퍼셉트론에 한 번에 한 개의 샘플이 주입되면 각 샘플에 대해 예측이 만들어지고,
=> 잘못된 예측을 하는 모든 출력 뉴런에 대해 올바른 예측을 만들 수 있도록 입력에 연결된 가중치를 강화시킴
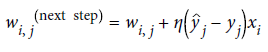
-
wi,j 는 i번째 입력 뉴런과 j번째 출력 뉴런 사이를 연결하는 가중치
-
xi는 현재 훈련 샘플의 i번째 뉴런의 입력값
-
yj-hat 은 현재 훈련 샘플의 j번째 출력 뉴런의 출력값
-
yi는 현재 훈련 샘플의 j번째 출력 뉴런의 타깃값
-
η는 학습률
- 각 출력 뉴런의 결정 경계는 선형이므로 퍼셉트론도 복잡한 패턴을 학습하지 못함
- 훈련 샘플이 선형적으로 구분될 수 있다면 이 알고리즘이 정답에 수렴함
=> 퍼셉트론 수렴 이론
TLU 네트워크를 구현한 Perceptron 클래스
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # 꽃잎의 길이와 너비
y = (iris.target == 0).astype(np.int) #부채붓꽃인가?
per_clf = Perceptron()
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5]])y_pred=> array([0])
- 퍼셉트론 학습 알고리즘은 확률적 경사 하강법과 매우 닮았음
- 사이킷런의 Perceptron 클래스는 매개변수가 loss='perceptron', learning_rate='constant', eta0=1(lr), penalty=None 인 SGDClassifier와 같음
- 퍼셉트론은 클래스 확률을 제공하지 않으며, 고정된 임계값을 기준으로 예측 생성
퍼셉트론은 일부 간단한 문제(ex. XOR 분류 문제)를 풀 수 없는 약점이 존재(다른 선형 분류기와 마찬가지로)
- 고수준 문제를 위해, 펴셉트론을 여러 개 쌓아올리면 일부 제약을 줄일 수 있음을 발견 => 다층 퍼셉트론
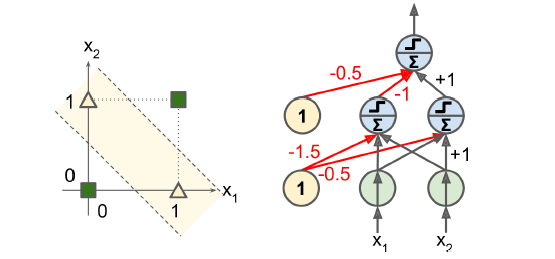
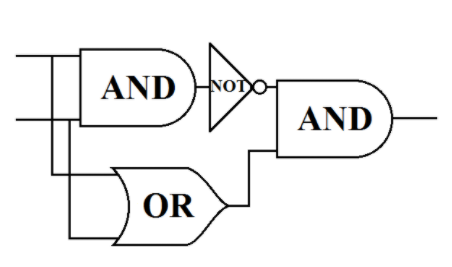
- 입력이 (0, 0)이나 (1, 1)일 때는 네트워크가 0을 출력하고
- 입력이 (0, 1)이나 (1, 0)일 때는 1을 출력
- 4개의 빨간색 연결을 제외하고 다른 모든 연결의 가중치는 1
=> NAND 게이트와 OR 게이트를 내재한 각각의 퍼셉트론이 다중 레이어 안에서 작동(은닉층)
=> 이 두 값에 AND 게이트를 수행한 출력층 결과가 최종 XOR 결과
10. 1. 4 다층 퍼셉트론과 역전파
다층 퍼셉트론의 구조
- 입력층 하나
- 은닉층이라 불리는 하나 이상의 TLU층
- 출력층
- 입력과 가까운 층을 하위 층, 출력에 가까운 층을 상위 층 이라고 부름
- 출력층을 제외하고 모든 층은 편향 뉴런을 포함하며 다음 층과 완전히 연결되어 있음
- 신호는 입력에서 출력 한 방향으로만 흐름 (피드포워드 신경망)
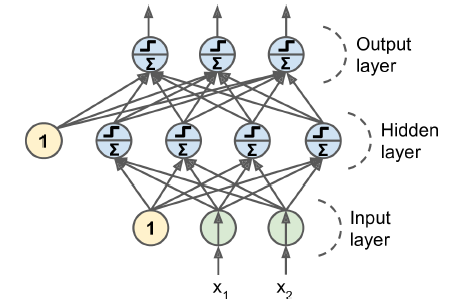
심층 신경망(DNN)
- 은닉층을 여러 개 쌓아 올린 인공 신경망
- 딥러닝은 심층 신경망을 연구하는 분야
역전파 훈련 알고리즘
- 다층 퍼셉트론을 훈련하는 방법
- 효율적인 기법으로 그래디언트를 자동으로 계산하는 경사 하강법
- 네트워크를 두 번(정방향 한 번, 역방향 한 번) 통과하는 것만으로 역전파 알고리즘은 모든 모델 파라미터에 대한 네트워크 오차의 그래디언트를 계산할 수 있음
(오차를 감소시키기 위해 각 연결 가중치와 편향값이 어떻게 바뀌어야 할지 알 수 있음)
- 그래디언트를 구하고 나면 평범한 경사 하강법 수행
- 전체 과정은 네트워크가 어떤 해결책으로 수렴될 때까지 반복
-
하나의 미니배치씩 진행하여 전체 훈련 세트를 처리하는 과정을 반복 (=> 각 반복을 epoch이라고 함)
-
각 미니배치는 네트워크 입력층으로 전달되어 첫 번째 은닉층으로 보내짐
-
미니배치에 있는 모든 샘플에 대해 해당 층에 있는 모든 뉴런의 출력을 계산함 -> 결과는 다음 층으로 전달
-
다시 이 층의 출력을 계산하고 결과는 다음 층으로 전달 -> 이런식으로 출력층을 계산할 때까지 계속됨
-
=> 정방향 계산
- 역방향 계산을 위해 중간 계산값을 모두 저장하는 것 외에는 예측을 만드는 것과 같음
-
-
알고리즘이 네트워크의 출력 오차를 측정 (손실 함수를 사용해 기대하는 출력과 네트워크의 실제 출력을 비교하고 오차 측정 값을 반환함)
-
각 출력 연결이 이 오차에 기여하는 정도를 계산
-
연쇄 법칙 적용
-
-
또 다시 연쇄 법칙을 사용해 이전 층의 연결 가중치가 이 오차의 기여 정도에 얼마나 기여했는지 측정
-
이렇게 입력층에 도달할 때까지 역방향으로 계속됨
-
이런 역방향 단계는 오차 그래디언트를 거꾸로 전파함으로써 네트워크에 있는 모든 연결 가중치에 대한 오차 그래디언트를 측정함
-
-
경사 하강법을 수행하여 방금 계산한 오차 그래디언트를 사용해 네트워크에 있는 모든 연결 가중치를 수정
요약하자면 다음과 같은 과정을 거침
-
각 훈련 샘플에 대해 역전파 알고리즘이 먼저 예측을 만들고 (정방향 계산)
-
오차를 측정
-
역방향으로 각 층을 거치면서 각 연결이 오차에 기여한 정도를 측정 (역방향 계산)
-
이 오차가 감소하도록 가중치를 조정 (경사 하강법 단계)
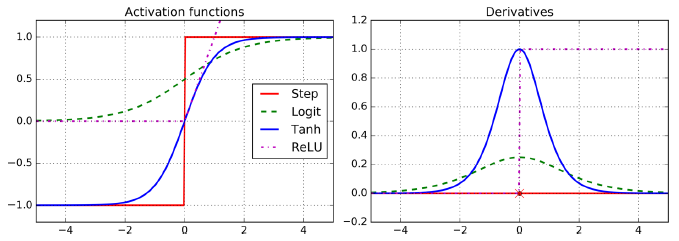
이 알고리즘을 잘 작동하고자 다층 퍼셉트론 구조에서 계단 함수를 로지스틱(시그모이드) 함수
σ(z) = 1 / (1 + exp(–z)) 로 바꿈
- 계단 함수에는 수평선밖에 없으니 계산할 그래디언트가 없음
- (경사하강법은 평편한 곳을 이동할 수 없음)
- 로지스틱 함수는 어디서든지 0이 아닌 그래디언트가 잘 정의되어 있음
- 역전파 알고리즘은 로지스틱 함수뿐만 아니라 다른 활성화 함수와도 사용될 수 있음
-
하이퍼볼릭 탄젠트 함수
- tanh(z) = 2σ(2z) - 1
- 로지스틱 함수처럼 S자 모양이고 연속적이며 미분 가능
- 하지만 출력 범위가 -1에서 1 사이 (로지스틱 함수 0~1)
- 이 범위는 각 층의 출력을 원점 근처로 모으는 경향이 있음(종종 빠르게 수렴되도록 도움)
-
ReLU 함수
- ReLU(z) = max(0, z)
- ReLU 함수는 연속적이지만 z=0에서 미분 가능하지 않음 (기울기가 갑자기 변해서 경사 하강법이 엉뚱한 곳으로 튈 수 있음)
- z<0 일 경우 도함수는 0
- 그러나 실제로는 잘 작동하고 계산 속도가 빨라 기본 활성화 함수가 되었음
- 출력에 최댓값이 없다는 점이 경사 하강법에 있는 일부 문제를 완화해줌
활성화 함수가 필요한 이유
- 선형 변환을 여러 개 연결해도 얻을 수 있는 것은 선형 변환뿐
- 층 사이에 비선형성을 추가하지 않으면 아무리 층을 많이 쌓아도 하나의 층과 동일해짐
=> 복잡한 문제를 풀 수 없음
- 비선형 활성화 함수가 있는 충분히 큰 심층 신경망은 이론적으로 어떤 연속 함수도 근사 가능
10. 1. 5 회귀를 위한 다층 퍼셉트론
다층 퍼셉트론은 회귀 작업에 사용 가능
- 값 하나를 예측하는 데 (ex. 여러 특성으로 주택 가격 예측 시) 출력 뉴런이 하나만 필요함
- 이 뉴런의 출력이 예측된 값
- 다변량 회귀(동시에 여러 값 예측)에서는 출력 차원마다 출력 뉴런이 하나씩 필요함
-
이미지에서 물체의 중심 위치를 파악하려면 2D 좌표를 예측해야 함 (=> 출력 뉴런 두 개 필요)
-
이 물체 주위로 바운딩 박스를 그리려면 물체의 너비와 높이를 나타내는 두 숫자가 더 필요함 (=> 출력 뉴런 4개 필요)
회귀용 다층 퍼셉트론을 만들 때 출력 뉴런에 활성화 함수를 사용하지 않고 어떤 범위의 값도 출력되도록 함
- 하지만 출력이 항상 양수여야 한다면, 출력층에 ReLU 활성화 함수를 사용할 수 있음
- 또는 softplus 활성화 함수를 사용함( softplus(z) = log(1+exp(x)) )
- 어떤 범위 안의 값을 예측하고 싶다면 로지스틱 함수나 하이퍼볼릭 탄젠트 함수를 사용
손실 함수
- 훈련에 사용하는 손실 함수는 전형적으로 평균 제곱 오차
- 훈련 세트에 이상치가 많다면 평균 절대값 오차 사용
- 이 둘을 조합한 후버 손실 사용 가능
10. 1. 6 분류를 위한 다층 퍼셉트론
이진 분류 문제에서는 로지스틱 활성화 함수를 가진 하나의 출력 뉴런만 필요 (출력 0~1 사이의 실수)
- 이를 양성 클래스에 대한 예측 확률로 해석 가능
- 음성 클래스에 대한 예측 확률은 1에서 양성 클래스의 예측 확률을 뺀 값
다중 레이블 이진 분류 문제 처리 가능
- 예를 들어 이메일의 스팸 여부와 긴급한 메일인지 동시에 예측하는 이메일 분류 시스템이 있다고 가정
- 이 경우 로지스틱 활성화 함수를 가진 두 출력 뉴런이 필요함
- 첫 번째 뉴런은 이메일이 스팸일 확률을 출력하고
- 두 번째 뉴런은 긴급한 메일일 확률을 출력함
(출력된 확률의 합이 1이 될 필요 없음)
- 모델은 어떤 레이블 조합도 출력할 수 있음
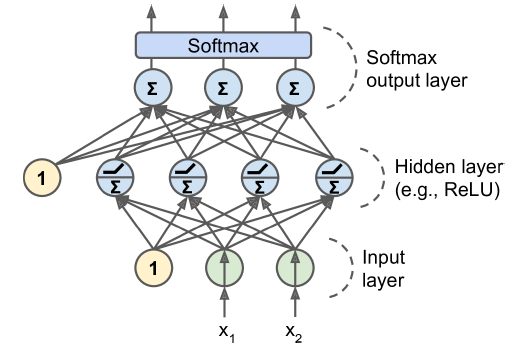
다중 분류
- 각 샘플이 3개 이상의 클래스 중 한 클래스에만 속할 수 있다면 클래스마다 하나의 출력 뉴런이 필요함
- 출력층에는 소프트맥스 활성화 함수를 사용해야함
- 소프트맥스 함수는 모든 예측 확률을 0과 1사이로 만들고 더했을 때 1이 되도록 만듦
(클래스가 서로 배타적일 경우 필요함)
손실 함수
- 확률 분포를 예측해야 하므로 손실 함수에는 크로스 엔트로피 손실(로그 손실, 4장 참고)를 선택하는 것이 좋음
[AI/Hands-on ML] - [핸즈온 머신러닝] 10장 - 케라스를 사용한 인공 신경망 2 (케라스로 딥러닝하기)
[핸즈온 머신러닝] 10장 - 케라스를 사용한 인공 신경망 2 (케라스로 딥러닝하기)
[AI/Hands-on ML] - [핸즈온 머신러닝] 10장 - 케라스를 사용한 인공 신경망 (인공 신경망 소개) [핸즈온 머신러닝] 10장 - 케라스를 사용한 인공 신경망 (인공 신경망 소개) 10. 인공 신경망 인공 신경망
kdeon.tistory.com
'AI > Hands-on ML' 카테고리의 다른 글
| [핸즈온 머신러닝] 10장 - 케라스를 사용한 인공 신경망 3 (하이퍼파라미터 튜닝) (0) | 2021.03.07 |
|---|---|
| [핸즈온 머신러닝] 10장 - 케라스를 사용한 인공 신경망 2 (케라스로 딥러닝하기) (0) | 2021.03.06 |
| [핸즈온 머신러닝] 9장 - 비지도 학습 2 (가우시안 혼합) (0) | 2021.02.05 |
| [핸즈온 머신러닝] 9장 - 비지도 학습 1 (군집) (0) | 2021.01.30 |
| [핸즈온 머신러닝] 8장 - 차원 축소 (0) | 2021.01.24 |
