8. 차원 축소
차원의 저주
- 많은 머신러닝 문제는 훈련 샘플이 각각 수천 수백만개의 특성을 가지고 있음
- 이런 많은 특성은 훈련을 느리게 할 뿐만 아니라, 좋은 솔루션을 찾기 어렵게 만듦
- 이러한 차원의 저주 문제들은 특성 수를 크게 줄여 불가능한 문제를 가능한 범위로 변경할 수 있음
-
MNIST 이미지처럼, 이미지 경계에 있는 픽셀은 거의 흰색이므로 훈련 세트에서 이런 픽셀을 제거해도 많은 정보를 잃지 않음
-
인접한 픽셀은 종종 많이 연관되어 있으므로, 두 픽셀을 하나로 합치더라도 잃는 정보가 많지 않음
훈련 속도를 높이는 것 외에 차원 축소는 데이터 시각화에도 유용
- 차원 수를 둘로 줄이면 고차원 훈련 세트를 하나의 압축된 그래프로 그릴 수 있으며,
- 군집 같은 시각적인 패턴을 감지해 통찰을 얻는 경우가 많음
8.1 차원의 저주

고차원 공간, 고차원 데이터셋
- 단위 면적(1x1 사각형)에서 임의의 두 점을 선택하면 두 점 사이의 거리는 평균적으로 대략 0.52
- 3차원 큐브에서 임의의 두 점을 선택하면 평균 거리는 대략 0.66
- 1,000,000차원의 초입방체에서 두 점을 무작위로 선택하면, 평균 거리는 약 407.25
->고차원은 많은 공간을 가지고 있기 때문
- 이로 인해 고차원 데이터셋은 매우 희박할 위험이 있음
- 즉, 대부분의 훈련 데이터가 서로 멀리 떨어져 있으며, 새로운 샘플도 훈련 샘플과 멀리 떨어져 있을 가능성이 높음
-
이 경우 예측을 위해 많은 외삽(extrapolation)을 해야하므로 저차원일 때보다 예측이 더 불안정
-
훈련 세트의 차원이 클수록 과대적합 위험이 커짐
차원의 저주를 해결하기 위해 훈련 샘플의 밀도가 충분히 높아질 때까지 훈련 세트의 크기를 키우는 이론적인 방법이 있지만, 훈련 샘플의 수가 기하급수적으로 늘어남
8. 2 차원 축소를 위한 접근 방법
차원을 감소시키는 두 가지 주요한 접근법, 투영과 매니폴드
8. 2. 1 투영
대부분 실전 문제는 훈련 샘플이 모든 차원에 걸쳐 균일하게 퍼져 있지 않음
- 많은 특성은 거의 변화가 없는 반면,
- 그 외 특성들은 서로 강하게 연관되어 있음
=> 모든 훈련 샘플이 고차원 공간 안의 저차원 부분 공간에 놓여 있음 (또는 가까이 놓여 있음)

- 모든 훈련 샘플이 거의 평면 형태로 놓여 있음 => 고차원(3D) 공간에 있는 저차원(2D) 부분 공간
- 모든 훈련 샘플을 이 부분 공간에 수직으로 (샘플과 평면 사이의 가장 짧은 직선을 따라) 투영하면 아래와 같은 2D 데이터 셋이 됨

- 데이터 셋 차원 3D -> 2D
- 각 축은 (평면에 투영된 자표인) 새로운 z1과 z2에 대응됨
투영이 언제나 최선의 방법은 아님

- 위 스위스 롤 데이터셋 처럼 부분 공간이 뒤틀리거나 휘어 있기도 함
- 그냥 평면에 투영시키면 (예를 들어 x3을 버리고) 아래 왼쪽 같은 2D 데이터셋을 얻게됨
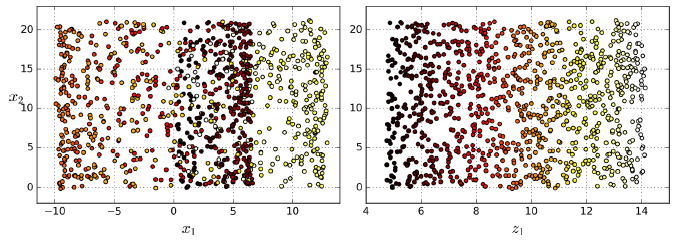
- 왼쪽 그래프는 보이는 것처럼 스위스 롤의 층이 서로 뭉개짐
- 우리는 오른쪽처럼 스위스 롤을 펼친 2D 데이터셋을 얻고자 함
8. 2. 2 매니폴드 학습
2D 매니폴드
- 스위스 롤은 2D 매니폴드의 한 예
- 2D 매니폴드는 고차원 공간에서 휘어지거나 뒤틀린 2D 모양
- d차원 매니폴드는 국부적으로 d차원 초평면으로 보일 수 있는 n차원 공간의 일부(d<n)
-
스위스 롤은 d=2 n=3 (국부적으로 2D 평면으로 보이지만 3차원으로 말려져 있음
매니폴드 학습
- 많은 차원 축소 알고리즘이 훈련 샘플이 놓여 있는 매니폴드를 모델하는 식으로 작동 -> 매니폴드 학습
- 대부분 실제 고차원 데이터셋이 더 낮은 저차원 매니폴드에 가깝게 놓여 있다는 매니폴드 가정 또는 매니폴드 가설에 근거
MNIST 데이터셋
- 전체 손글씨 숫자 이미지는 어느 정도 비슷함 (선으로 연결, 경계는 흰색, 어느정도 중앙)
- 무작위로 생성된 이미지라면 아주 적은 일부만 손글씨 숫자처럼 보임
- 숫자 이미지를 만들 때 가능한 자유도는 아무 이미지나 생성할 때의 자유도보다 훨씬 낮음
=> 이런 제약은 데이터셋을 저차원 매니폴드로 압축할 수 있도록 도와줌
매니폴드 가정
- 매니폴드 가정은 종종 암묵적으로 다른 가정과 병행되곤 함
=> 처리해야 할 작업(예를들면 분류나 회귀)이 저차원의 매니폴드 공간에 표현되면 더 간단해질 것이란 가정

- 예를 들어, 위 그림의 첫 번째 행에서는 스위스 롤이 두개의 클래스로 나누어 있음
- 3D (왼쪽)에서는 결정 경계가 매우 복잡하지만
- 펼쳐진 매니폴드 공간인 2D (오른쪽)에서는 결정 경계가 단순한 직선
- 이러한 암묵적인 가정이 항상 유효하지는 않음
- 두번째 행의 경우 결정 경계가 x1=5에 놓여 있음
- 이 결정 경계는 3D 공간에서는 매우 단순(수직 평면)
- 하지만 펼쳐진 매니폴드에서는 결정 경계가 더 복잡해짐(네 개의 독립된 수직선)
모델을 훈련시키기 전에 훈련 세트의 차원을 감소시키면 훈련 속도는 빨라지지만,
항상 더 낫거나 간단한 솔루션이 되는 것은 아님
-> 데이터셋에 달려있음
다음은 가장 널리 알려진 차원 축소 알고리즘 중 일부를 살펴봄
8. 3 PCA
주성분 분석 (PCA, Principal Component Analysis)
- 가장 인기 있는 차원 축소 알고리즘
- 데이터에 가장 가까운 초평면을 정의한 후, 데이터를 이 평면에 투영시킴
8. 3. 1 분산 보존
저차원의 초평면에 훈련 세트를 투영하기 전, 올바른 초평면을 선택해야 함

- 왼쪽 그래프는 간단한 2D 데이터셋이 세 개의 축과 함께 표현되어 있음
- 오른쪽 그래프는 데이터셋이 각 축에 투영된 결과임
- 실선에 투영된 것은 분산을 최대로 보존하는 반면,
- 점선에 투영된 것은 분산을 매우 적게 유지하고 있음
- 가운데 파선에 투영된 것은 중간 정도로 분산을 유지하고 있음
다른 방향으로 투영하는 것보다 분산이 최대로 보존하는 축을 선택하는 것이 정보가 가장 적게 손실되므로 합리적으로 보임
- 원본 데이터셋과 투영된 것 사이의 평균 제곱 거리를 최소화하는 축
8. 3. 2 주성분
PCA는 훈련 세트에서 분산이 최대인 축을 찾음
- 위 그림에서는 실선
- 또한 첫 번째 축에 직교하고 남은 분산을 최대로 보존하는 두 번째 축을 찾음
-
이 2D 예제에서는 선택의 여지가 없음 => 점선이 됨
- 고차원 데이터셋이라면 PCA는 이전의 두 축에 직교하는 세 번째 축을 찾으며
- 데이터셋에 있는 차원의 수만큼 n번재 축을 찾음
i번째 축을 이 데이터의 i번째 주성분(PC)라고 부름
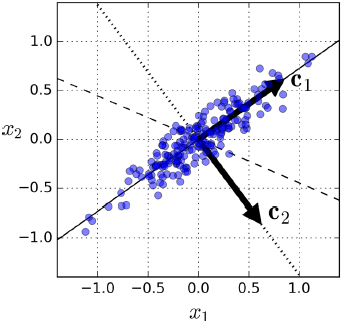
- 위 그림에서 첫번째 PC는 벡터 c1이 놓인 축이고
- 두 번째 PC는 벡터 c2가 놓인 축

- 아까 보았던 이 그림에서는 처음 두개의 PC는 두 화살표가 놓인 평면의 수직 축임
- 세 번째 PC는 이 평면에 수직임
※ 각 주성분을 위해 PCA는 주성분 방향을 가리키고 원점에 중앙이 맞춰진 단위 벡터를 찾음
- 하나의 축에 단위 벡터가 반대 방향으로 두개 있으므로 PCA가 반환하는 단위 벡터의 방향은 일정하지 않음
- 주성분의 방향은 일정하지 않음
특잇값 분해(SVD)
- 훈련 세트의 주성분을 찾는 방법
- 표준 행렬 분해 기술로, 훈련 세트 행렬 X를 세 개 행렬의 행렬 곱셈인 UΣV^T 로 분해할 수 있음
- 여기서 찾고자 하는 모든 주성분의 단위 벡터가 V에 다음과 같이 담겨 있음

svd()함수를 사용해 훈련 세트의 모든 주성분을 구한 후 처음 두개의 PC를 정의하는 두 개의 단위 벡터를 추출하는 코드
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]- PCA는 데이터셋의 평균이 0이라고 가정
- 사이킷런의 PCA 파이썬 클래스는 이 작업을 대신 처리하지만, PCA는 구현하거나 다른 라이브러리를 사용한다면 먼저 데이터를 원점에 맞추어야 함
8. 3. 3 d차원으로 투영하기
주성분을 모두 추출했다면, 처음 d개의 주성분으로 정의한 초평면에 투영하여 데이터셋의 차원을 d차원으로 축소 할 수 있음
- 이 초평면은 분산을 가능한 한 최대로 보존하는 투영을 보장
초평면에 훈련 세트를 투영하고 d차원으로 축소된 데이터셋 Xd-proj 을 얻기 위해서는 아래와 같이 행렬 X와 V의 첫 d열로 구성된 행렬 Wd를 행렬 곱셈하면 됨
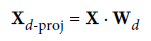
다음 코드는 첫 두 개의 주성분으로 정의된 평면에 훈련 세트를 투영함
W2 = Vt.T[:, :2]
X2D = X_centered.dot(W2)
8. 3. 4 사이킷런 사용하기
사이킷런의 PCA 모델은 SVD 분해 방법을 사용하여 구현
PCA모델을 사용해 데이터셋의 차원을 2로 줄이는 코드
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X2D = pca.fit_transform(X)PCA 변환기를 데이터셋에 학습시키면, components_ 속성에 W^d의 전치가 담겨 있음
(ex. 첫 번째 주성분을 정의하는 단위 벡터는 pca.components_.T[:, 0])
8. 3. 5 설명된 분산의 비율
주성분의 설명된 분산의 비율은 explained_variance_ratio_ 변수에 저장되어 있음
- 이 비율은 각 주성분의 축을 따라 있는 데이터셋의 분산 비율을 나타냄
pca.explained_variance_ratio_=> array([0.84248607, 0.14631839])
- 데이터셋 분산의 84.2%가 첫 번째 PC를 따라 놓여 있고,
- 14.6%가 두 번째 PC를 따라 놓여 있음
- 세 번째 PC에는 1.2% 미만이 남아 있을 것이므로 아주 적은 양의 정보가 들어있을 것
8. 3. 6 적절한 차원 수 선택하기
축소할 차원의 수를 임의로 정하기 보다는
충분한 분산(ex. 95%)이 될 때까지 더해야 할 차원 수를 선택하는 것이 간단함
(데이터 시각화를 위해 축소하는 경우 차원을 2~3개로 줄이는 것이 일반적)
차원을 축소하지 않고 PCA를 계산한 뒤 훈련 세트의 분산을 95%로 유지하는 데 필요한 최소한의 차원 수를 계산하는 코드
pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1n_components=d로 설정하여 PCA를 다시 실행
- 유지하려는 주성분의 수를 지정하기보다는,
- 분산의 비율을 n_components에 0.0에서 1.0 사이로 설정하는 편이 나음
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)또 다른 방법은 설명된 분산을 차원 수에 대한 함수로 그리는 것 (cumsum을 그래프로 그림)
- 이 그래프에는 설명된 분산의 빠른 성장이 멈추는 변곡점이 있음
- 여기서는 차원을 약 100으로 축소해도 설명된 분산을 크게 손해 보지 않음

8. 3. 7 압축을 위한 PCA
차원을 축소하고 난 후에는 훈련 세트의 크기가 줄어듦
MNIST 데이터셋에 분산의 95%를 유지하도록 PCA적용
- 각 샘플은 원래의 784개 특성이 아닌 150개 정도 가지고 있을 것
- 대부분 분산은 유지되었지만 데이터셋은 원본 크기의 20% 미만이 됨
=> 상당한 압축률, 이런 크기 축소는(SVM 같은) 분류 알고리즘의 속도를 크게 높일 수 있음
압축된 데이터셋에 PCA 투영의 변환을 반대로 적용하여 784개의 차원으로 되돌릴 수도 있음
- 투영에서 일정량의 정보(유실된 5%의 분산)를 잃어버렸기 때문에 이렇게 해도 원본 데이터셋을 얻을 수 없음
- 그러나 원본 데이터와 매우 비슷
- 원본 데이터와 재구성된 데이터 사이의 평균 제곱 거리를 재구성 오차 라고 함
MNIST 데이터셋을 154 차원으로 압축하고 inverse_transform() 메서드를 사용해 784차원으로 복원
pca = PCA(n_components = 154)
X_reduced = pca.fit_transform(X_train)
X_recovered = pca.inverse_transform(X_reduced)
원본 훈련 세트와 샘플을 압축한 후 복원한 결과

역변환 공식

8. 3. 8 랜덤 PCA
확률적 알고리즘을 사용해 처음 d개의 주성분에 대한 근삿값을 빠르게 찾음
- 사이킷런 svd_solver 매개변수를 "randomized" 로 지정
- 계산 복잡도는 완전한 SVD 방식인 O(m × n^2) + O(n^3)이 아닌, O(m × d^2) + O(d^3)
- 따라서 d가 n보다 많이 작으면 완전 SVD보다 훨씬 빠름
rnd_pca = PCA(n_components=154, svd_solver="randomized", random_state=42)
X_reduced = rnd_pca.fit_transform(X_train)- svd_solver의 기본값은 "auto"
- m이나 n이 500보다 크로 d가 m이나 n의 80%보다 작으면 사이킷런은 자동으로 랜덤 PCA 알고리즘 사용
- 아니면 완전한 SVD 방식을 사용 (svd_solver="full")
8. 3. 9 점진적 PCA
PCA 구현의 문제는 SVD 알고리즘을 실행하기 위해 전체 훈련 세트를 메모리에 올려야 한다는 것
-> 점진적 PCA 알고리즘으로 해결
점진적 PCA는 훈련 세트를 미니배치로 나눈 뒤 IPCA 알고리즘에 한 번에 하나씩 주입
- 훈련 세트가 클 때 유용하고 온라인으로 PCA를 적용할 수 있음 (새로운 데이터가 준비되는 대로 실시간 PCA 적용 가능)
MNIST 데이터셋을 100개의 미니배치로 나누고 IncrementalPCA 클래스에 주입하여 데이터셋의 차원을 154개로 줄이는 코드
from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
print(".", end="") # not shown in the book
inc_pca.partial_fit(X_batch)
X_reduced = inc_pca.transform(X_train)
또 다른 방법은 넘파이의 mammap 클래스를 사용해 하드 디스크의 이진 파일에 저장된 매우 큰 배열을 메모리에 들어 있는 것처럼 다루는 것
- 이 클래스는 필요할 때 데이터를 메모리에 적재
- IncrementalPCA는 특정 순간에 배열의 일부만 사용하기 때문에 메모리 무족 문제를 해결 가능
- fit() 메서드 사용 가능
X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n))
batch_size = m // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mm)
8. 4 커널 PCA
커널 트릭
샘플을 매우 높은 고차원 공간(특성 공간)으로 암묵적으로 매핑하여 서포트 벡터 머신의 비선형 분류와 회귀를 가능하게 하는 수학적 기법 (5장 참고)
-> 고차원 특성 공간에서의 선형 결정 경계는 원본 공간에서는 복잡한 비선형 결정 경계에 해당함
커널 PCA
같은 기법을 PCA에 적용해 차원 축소를 위한 복잡한 비선형 투형 수행 가능
- 투영된 후 샘플의 군집을 유지하거나 꼬인 매니폴드에 가까운 데이터셋을 펼칠 때도 유용
KernelPCA를 사용해 RBF 커널로 kPCA 적용
from sklearn.decomposition import KernelPCA
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.04)
X_reduced = rbf_pca.fit_transform(X)
선형 커널, RBF 커널, 시그모이드 커널을 사용하여 2차원으로 축소시킨 스위스 롤

8. 4. 1 커널 선택과 하이퍼파라미터 튜닝
- kPCA는 비지도 학습이므로, 좋은 커널과 하이퍼파라미터 선택을 위한 명확한 성능 측정 기준이 없음
- 차원 축소는 종종 지도 학습(ex. 분류)의 전처리 단계로 활용되므로 그리드 탐색을 사용하여 주어진 문제에서 성능이 가장 좋은 커널과 하이퍼파라미터를 선택할 수 있음
- 다음 코드는 두 단계의 파이프라인으로,
- 먼저 kPCA를 사용해 차원을 2차원으로 축소하고
- 분류를 위해 로지스틱 회귀를 적용
- 그 후 파이프라인 마지막 단계에서 가장 높은 분류 정확도를 얻기 위해 GridSearchCV를 사용해 kPCA의 가장 좋은 커널과 gamma 파라미터를 찾음
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
clf = Pipeline([
("kpca", KernelPCA(n_components=2)),
("log_reg", LogisticRegression(solver="lbfgs"))
])
param_grid = [{
"kpca__gamma": np.linspace(0.03, 0.05, 10),
"kpca__kernel": ["rbf", "sigmoid"]
}]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)가장 좋은 커널, 하이퍼파라미터는 best_params_ 변수에 저장됨
print(grid_search.best_params_)=> {'kpca__gamma': 0.043333333333333335, 'kpca__kernel': 'rbf'}
재구성
완전한 비지도 학습 방법으로, 가장 낮은 재구성 오차를 만드는 커널과 하이퍼파라미터를 선택하는 방식도 있음
- 재구성은 선형 PCA만큼 쉽지 않음
- 스위스롤의 원본 3D 데이터셋(왼쪽 위)과 RBF 커널의 kPCA를 적용한 2D 데이터셋(오른쪽 위)을 보여줌
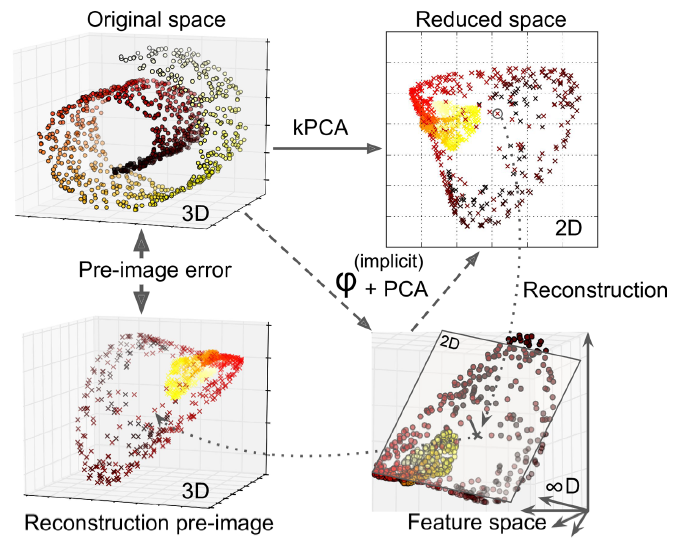
- 커널 트릭 덕분에 이 변환은 특성 맵φ을 사용하여 훈련 세트를 무한 차원의 특성 공간(오른쪽 아래)에 매핑한 다음, 변환된 데이터셋을 선형 PCA를 사용해 2D로 투영한 것과 수학적으로 동일
- 축소된 공간에 있는 샘플에 대해 선형 PCA를 역전시키면 재구성된 데이터 포인트는 원본 공간이 아닌 특성 공간에 놓이게 됨
-
이 특성 공간은 무한 차원으로 재구성된 포인트를 계산할 수 없고 실제 에러 계산 불가
-
다행히 재구성된 포인트에 가깝게 매핑된 원본 공간의 포인트를 찾을 수 있음 => 재구성 원상
-
원상을 얻게 되면 원본 샘플과의 제곱 거리 추정 가능
-
-> 재구성 원상의 오차를 최소화하는 커널과 하이퍼파라미터를 선택할 수 있음
재구성 방법
- 투영된 샘플을 훈련 세트로, 원본 샘플을 타깃으로 하는 지도 학습 회귀 모델 훈련
- 사이킷런 fit_inverse_transform=True 지정시 이를 자동으로 수행
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433,
fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)- 재구성 원상 오차 계산
from sklearn.metrics import mean_squared_error
mean_squared_error(X, X_preimage)=> 32.78630879576612
- 재구성 원상 오차를 최소화하는 커널과 하이퍼파라미터를 찾기 위해 교차 검증으로 그리드 탐색 사용 가능
8. 5 LLE
지역 선형 임베딩 (LLE, Locally Linear embedding)
또 다른 강력한 비선형 차원 축소(NLDR) 기술
- 이전 알고리즘처럼 투영에 의존하지 않는 매니폴드 학습
- LLE는 각 훈련 샘플이 가장 가까운 이웃(c.n)에 얼마나 선형적으로 연관되어 있는지 측정
- 그 후 국부적인 관계가 가장 잘 보존되는 훈련 세트의 저차원 표현을 찾음
- 잡음이 너무 많지 않은 경우 꼬인 매니폴드를 펼치는 데 잘 작동하는 방법

1. 데이터 포인트 Xi에 대해 Xi과 가장 가까운 k개의 이웃점 Xj들을 선택
2. Xj로 부터 Xi를 가장 잘 재구성하는 가중치 Wij를 구함
- 이때 가중치 Wij는 데이터 포인트 Xi와 Xj 들간의 지역 선형 관계를 나타냄
3. 이러한 관계가 최대한 보존 되도록 데이터를 저차원인 d차원 공간으로 매핑
※ 이에 대한 자세한 과정은 아래에서 추가 설명
LocallyLinearEmbedding 클래스를 사용한 스위스 롤 펼치기
from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_reduced = lle.fit_transform(X)
결과 2D 데이터셋
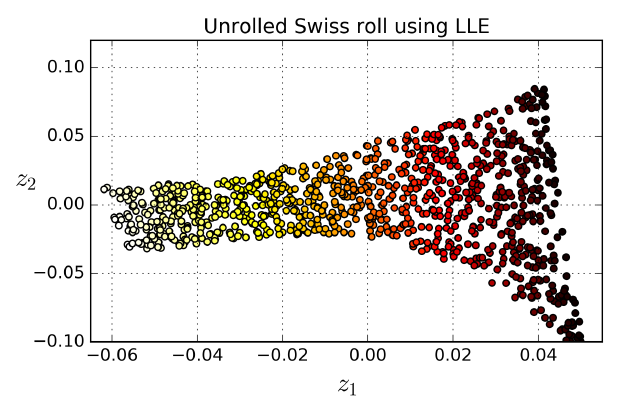
- 스위스 롤이 완전히 펼쳐졌고, 지역적으로는 샘플 간 거리가 잘 보존되어 있음
- 반면에 크게 보면 샘플 간 거리가 잘 유지되어 있지 않음
- 펼쳐진 스위스 롤의 오른쪽은 압축되어 있고, 왼쪽은 확장되어 있음
-> 그럼에도 불구하고, LLE는 매니폴드를 모델링하는 데 잘 동작함
LLE가 작동하는 방식
1. 먼저 알고리즘이 각 훈련 샘플 x(i)에 대해 가장 가까운 k개의 샘플을 찾음 (앞 코드에선 k=10)
- 그런 다음, 이 이웃에 대한 선형 함수로 x(i)를 재구성
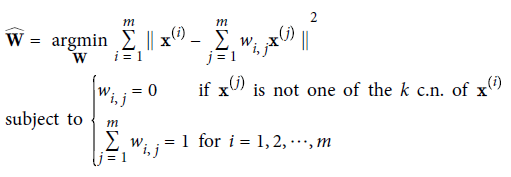
- x(j)가 x(i)의 가장 가까운 k개 이웃 중 하나가 아닐 경우, wi,j = 0 이 됨
- 그러므로 LLE는 첫 단계는 위 식과 같은 제한이 있는 최적화 문제가 됨
- W는 가중치 wi,j를 모두 담은 가중치 행렬
- 두 번째 제약은 각 훈련 샘플 x(i)에 대한 가중치를 단순히 정규화하는 것
- 이 단계를 거치면 (가중치 wi,j-hat를 담은) 가중치 행렬 W-hat은 훈련 샘플 사이에 있는 지역 선형 관계를 담고 있음
2. 두 번째 단계는 가능한 한 이 관계가 보존되도록 훈련 샘플을 d차원 공간(d<n)으로 매핑
- 만약 z(i)가 d차원 공간에서 x(i)의 상(image)이라면 가능한 한 z(i)와 Σ wi,j-hat * z(j) 사이의 거리가 최소화 되어야 함(아래 식 참고)
- 이는 아래 식과 같은 제약이 없는 최적화 문제로 바꾸어줌
- 첫 번째 단계는 샘플을 고정하고 최적의 가중치를 찾지만, 두 번째 단계에서는 가중치를 고정하고 저차원의 공간에서 샘플 이미지의 최적 위치를 찾음
- Z는 모든 z(i)를 포함하는 행렬

사이킷런이 제공하는 LLE 구현의 계산 복잡도는 k개의 가장 가까운 이웃을 찾는 데 O(m log(m)n log(k)),
가중치 최적화에 O(mnk^3), 저차원 표현을 만드는데 O(dm^2)
- 마지막 항의 m^3 때문에 이 알고리즘을 대량의 데이터 셋에 적용하기 어려움
8. 6 다른 차원 축소 기법
랜덤 투영
랜덤한 선형 투영을 사용해 데이터를 저차원 공간으로 투영
- 이러한 랜덤 투영이 실제로 거리를 잘 보존함
- 차원 축소 품질은 샘플 수와 목표 차원수에 따라 다르며, 초기 차원수에는 의존적이지 않음
다차원 스케일링(MDS)
샘플 간의 거리를 보존하면서 차원을 축소
Isomap
각 샘플을 가장 가까운 이웃과 연결하는 식으로 그래프를 만듦
- 그 후 샘플 간의 지오데식 거리를 유지하면서 차원을 축소
t-SNE
비슷한 샘플은 가까이, 비슷하지 않은 샘플은 멀리 떨어지도록 하면서 차원을 축소
- 주로 시각화에 많이 사용
- 특히 고차원 공간에 있는 샘플의 군집을 시각화할 때 사용
(ex. MNIST 데이터셋을 2D로 시각화할 때)
선형 판별 분석(LDA)
분류 알고리즘이지만, 훈련 과정에서 클래스 사이를 가장 잘 구분하는 축을 학습함
- 이 축은 데이터가 투영되는 초평면을 정의하는 데 사용 가능
- 투영을 통해 가능한 한 클래스를 멀리 떨어지게 유지시키므로 SVM 분류기 같은 다른 분류 알고리즘을 적용하기 전에 차원을 축소시키는 데 좋음

참고
PCA
bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-9-PCA-Principal-Components-Analysis
LLE [논문]
www.robots.ox.ac.uk/~az/lectures/ml/lle.pdf
이번 장은 유독 개념 이해를 위해 생략할 수 있는 내용이 거의 없었다.
추가적으로 공부해 쉽게 정리할 필요가 있을 것 같음.
'AI > Hands-on ML' 카테고리의 다른 글
| [핸즈온 머신러닝] 9장 - 비지도 학습 2 (가우시안 혼합) (0) | 2021.02.05 |
|---|---|
| [핸즈온 머신러닝] 9장 - 비지도 학습 1 (군집) (0) | 2021.01.30 |
| [핸즈온 머신러닝] 핸즈온 머신러닝2 정오표 (0) | 2021.01.22 |
| [핸즈온 머신러닝] 7장 - 앙상블 학습과 랜덤 포레스트 (0) | 2021.01.19 |
| [핸즈온 머신러닝] 6장 - 결정 트리 (0) | 2021.01.03 |
