[AI/Hands-on ML] - [핸즈온 머신러닝] 9장 - 비지도 학습 1 (군집)
[핸즈온 머신러닝] 9장 - 비지도 학습 1 (군집)
9. 비지도 학습 - 많은 데이터는 대부분 레이블이 없음 - 레이블을 부여하는 작업은 비용이 크며 오래걸림 => 레이블이 없는 데이터를 바로 사용하기 위한 비지도 학습 9. 1 군집 비슷한 샘플을 구
kdeon.tistory.com
9. 2 가우시안 혼합
가우시안 혼합 모델
샘플이 파라미터가 알려지지 않는 여러 개의 혼합된 가우시안 분포에서 생성되었다고 가정하는 확률 모델
하나의 가우시안 분포에서 생성된 모든 샘플은 하나의 클러스터를 형성

사이킷런의 GaussianMixture 클래스
- 사전에 가우시안 분포의 개수 k를 알아야 함
- 데이터셋 X가 다음 확률 과정을 통해 생성되었다고 가정
-
샘플마다 k개의 클러스터에서 랜덤하게 한 클러스터가 선택되고
-
j번째 클러스터를 선택할 확률은 클러스터의 가중치 φ(j) 로 정의됨
-
i번째 샘플을 위해 선택한 클러스터 인덱스는 z(i)
-
z(i)=j 이면, (i번째 샘플이 j번째 클러스터에 할당되었다면) 이 샘플의 위치 x(i)는 평균이 μ(j)이고 공분산 행렬이 Σ(j)인 가우시안 분포에서 랜덤하게 샘플링됨
- 데이터셋 X가 주어지면 가중치 φ와 전체 분포의 파라미터 μ(1)에서 μ(k)까지와 Σ(1)에서 Σ(k)까지를 추정하는 코드
from sklearn.mixture import GaussianMixture
gm = GaussianMixture(n_components=3, n_init=10, random_state=42)
gm.fit(X)gm.weights_=> array([0.20965228, 0.4000662 , 0.39028152])
- 실제 이 데이터를 생성하기 위해 사용한 가중치는 0.2, 0.4, 0.4
gm.means_=> array([[ 3.39909717, 1.05933727], [-1.40763984, 1.42710194], [ 0.05135313, 0.07524095]])
gm.covariances_=> array([[[ 1.14807234, -0.03270354], [-0.03270354, 0.95496237]], [[ 0.63478101, 0.72969804], [ 0.72969804, 1.1609872 ]], [[ 0.68809572, 0.79608475], [ 0.79608475, 1.21234145]]])
위 클래스는 기댓값-최대화(Expectation-Maximization, EM) 알고리즘을 사용함
- 클러스터 파라미터를 랜덤하게 초기화하고 수렴할때까지 두 단계를 반복함
-
먼저 샘플을 클러스터에 할당 (기댓값 단계)
-
그 후 클러스터를 업데이트 (최대화 단계)
-
군집 입장에서 보면 EM을 클러스터 중심 (μ(1)에서 μ(k)까지) 뿐만 아니라 크기, 모양, 방향 (Σ(1)에서 Σ(k)까지)과 클러스터의 상대적 가중치 (φ(1)에서 φ(k)까지) 를 찾는 k-평균의 일반화로 생각할 수 있음
- k-평균과 달리 EM은 하드 클러스터 할당이 아니라 소프트 클러스터 할당을 사용함
-
기댓값 단계에서 알고리즘은 각 클러스터에 속할 확률을 예측함
-
그 다음 최대화 단계에서 각 클러스터가 데이터셋에 있는 모든 샘플을 사용해 업데이트됨
-
클러스터에 속할 추정 확률로 샘플에 가중치가 적용됨 (이 확률을 샘플에 대한 클러스터의 책임 이라고 부름)
※ k-평균과 마찬가지로 EM도 나쁜 솔루션으로 수렴할 수 있음
- 여러 번 실행하여 가장 좋은 솔루션을 선택해야함 (n_init 값 설정)
# 알고리즘이 수렴했는지 여부
gm.converged_=> True
# 반복 횟수
gm.n_iter_
=> 3
각 클러스터의 위치, 크기, 모양, 방향, 상대적인 가중치을 예측했으므로,
- 이 모델은 새로운 샘플을 가장 비슷한 클러스터에 쉽게 할당할 수 있음(하드 군집) => predict()
- 또는 특정 클러스터에 속할 확률을 예측할 수 있음(소프트 군집) => predict_proba()
gm.predict(X)=> array([2, 2, 1, ..., 0, 0, 0])
gm.predict_proba(X)=> array([[2.32389467e-02, 6.77397850e-07, 9.76760376e-01], [1.64685609e-02, 6.75361303e-04, 9.82856078e-01], [2.01535333e-06, 9.99923053e-01, 7.49319577e-05], ..., [9.99999571e-01, 2.13946075e-26, 4.28788333e-07], [1.00000000e+00, 1.46454409e-41, 5.12459171e-16], [1.00000000e+00, 8.02006365e-41, 2.27626238e-15]])
가우시안 혼합 모델은 생성 모델
- 이 모델에서 새로운 샘플을 만들 수 있음
X_new, y_new = gm.sample(6)
X_new=> array([[ 2.95400315, 2.63680992], [-1.16654575, 1.62792705], [-1.39477712, -1.48511338], [ 0.27221525, 0.690366 ], [ 0.54095936, 0.48591934], [ 0.38064009, -0.56240465]])
y_new=> array([0, 1, 2, 2, 2, 2])
또는 주어진 위치에서 모델의 밀도를 추정할 수 있음 -> score_samples() 사용
- 샘플이 주어지면 이 메서드는 그 위치의 확률 밀도 함수(PDF)의 로그를 예측함
- 점수가 높을수록 밀도가 높음
gm.score_samples(X)=> array([-2.60782346, -3.57106041, -3.33003479, ..., -3.51352783, -4.39802535, -3.80743859])
- 이 점수의 지숫값을 계산하면 샘플의 위치에서 PDF값을 얻을 수 있음
- 이 값은 하나의 확률이 아니라 확률 밀도임(어떠한 양숫값도 될 수 있음)

알고리즘이 훌륭한 솔루션을 찾은 것으로 보임
- 하지만 이 문제는 2D 가우시안 분포를 사용해 데이터를 생성한 쉬운 작업
- 실제 데이터는 가우시안 분포나 저차원이 아닌 경우가 많음
- 또한 이 알고리즘에 정확한 클러스터 개수를 입력했음
- 특성이나 클러스터가 많거나 샘플이 적을 때는 EM이 최적의 솔루션으로 수렴하기 어려움
- 이런 작업의 어려움을 줄이려면 알고리즘이 학습할 파라미터 개수를 제한해야 함
-
클러스터의 모양과 방향의 범위를 제한할 수 있음 => 공분산 행렬에 제약 추가
-
사이킷런에서는 covariance_type 매개변수 설정
-
spherical : 모든 클러스터가 원형이지만, 지름은 다를 수 있음 (분산이 다름)
-
diag : 클러스터는 크기에 상관없이 어떤 타원형도 가능함. 하지만 타원의 축은 좌표 축과 나란해야 함 (공분산 행렬이 대각 행렬이어야 함)
-
tied : 모든 클러스터가 동일한 타원 모양, 크기, 방향을 가짐 (모든 클러스터는 동일한 공분산 행렬 공유)
-
full : 기본값, 각 클러스터는 모양, 크기, 방향에 제약이 없음 (즉, 각자 제약이 없는 공분산 행렬을 가짐)
-

※ 계산 복잡도
GaussianMixture 모델을 훈련하는 계산 복잡도는 샘플 개수 m, 차원 개수 n, 클러스터 개수 k와 공분산 행렬에 있는 제약에 따라 결정됨
- "spherical" 나 "diag" 이면 데이터에 어떤 클러스터 구조가 있다고 가정하므로 O(kmn)
- "tied" 나 "full" 이면 O(kmn^3+kn^3)
=> 특성 개수가 많으면 적용하기 어려움
9. 2. 1 가우시안 혼합을 사용한 이상치 탐지
이상치 탐지는 보통과 많이 다른 샘플을 감지하는 작업
보통 샘플은 정상치라고 함
가우시안 혼합 모델을 이상치 탐지에 사용하는 방법은, 밀도가 낮은 지역에 있는 모든 샘플을 이상치로 간주하는 것
-> 사용할 밀도 임계값을 정해야함
- 거짓양성이 많다면 임계값을 낮추고, 거짓음성이 많다면 임계값을 높임 (정밀도/재현율 트레이드 오프)
네 번째 백분위수(4%)를 밀도 임계값으로 사용하여 이상치를 구분하는 코드
densities = gm.score_samples(X)
density_threshold = np.percentile(densities, 4)
anomalies = X[densities < density_threshold]
이와 비슷한 특이치 탐지는 이상치로 오염되지 않는 깨끗한 데이터셋에서 훈련한다는 것이 이상치 탐지와 다른 점
- 이상치 탐지는 이런 가정을 하지 않고, 데이터셋을 정제하는 데 자주 사용됨
※ 가우시안 혼합 모델은 이상치를 포함해 모든 데이터에 맞추려고함
- 따라서 이상치가 너무 많으면 모델이 정상치를 바라보는 시각이 편향되고, 일부 이상치를 정상으로 잘못 생각할 수 있음
- 이런 경우는 먼저 한 모델을 훈련하고 가장 크게 벗어난 이상치를 제거해 그 다음 정제된 데이터셋에서 모델을 다시 훈련함
9. 2. 2 클러스터 개수 선택하기
k-평균에서는 이너셔나 실루엣 점수를 사용해 적절한 클러스터 개수를 선택하지만,
가우시안 혼합에서는 이런 지표를 사용할 수 없음
- 이런 지표들은 클러스터가 타원형이거나 크기가 다를 때 안정적이지 않기 때문
대신 아래 BIC 나 AIC 와 같은 이론적 정보 기준을 최소화하는 모델을 찾음
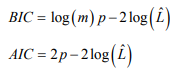
m : 샘플의 개수
p : 모델이 학습할 파라미터 개수
L-hat : 모델의 가능도 함수의 최댓값
BIC와 AIC는 모두 학습할 파라미터가 많은(=클러스터가 많은) 모델에게 벌칙을 가하고 데이터에 잘 학습하는 모델에게 보상을 더함
- 이 둘은 종종 동일한 모델을 선택함
- 둘의 선택이 다를 경우 BIC가 선택한 모델이 AIC가 선택한 모델보다 간단한(=파라미터가 적은) 경향이 있음
- 하지만 데이터가 아주 잘 맞지 않을 수 있음(특히 대규모 데이터셋)
가능도 함수
확률과 가능도는 종종 구별 없이 사용되지만, 통계학에서 이 둘은 다른 의미를 가짐
- 파라미터 0인 확률 모델이 주어지만 '확률'은 미래 출력 x가 얼마나 그럴듯한지 설명함 (파라미터 값 0을 알고 있다면)
- '가능도'는 출력 x를 알고 있을 때 특정 파라미터 값 0이 얼마나 그럴듯한지 설명함
BIC와 AIC 계산
gm.bic(X)
gm.aic(X)=> 8189.74345832983
=> 8102.518178214792

위 그래프에서 볼 수 있듯이
- k=3 에서 BIC 와 AIC 모두 가장 작으므로 k=3이 최선의 선택으로 보임
- covaraince_type 매개변수에 대해 최선의 값을 탐색할 수도 있음
-
예를 들어 "full" 대신 "spherical"을 선택하면
-
학습할 파라미터가 크게 줄어들지만 데이터에 잘 맞지 않음
9. 2. 3 베이즈 가우시안 혼합 모델
최적의 클러스터 개수를 수동으로 찾지 않고 불필요한 클러스터의 가중치를 0으로 (또는 0에 가깝게) 만드는 BayesianGaussianMixture 클래스를 사용할 수 있음
- 클러스터 개수 n_components를 최적의 클러스터 개수보다 크다고 믿을 만한 값으로 지정
- 이 알고리즘은 자동으로 불필요한 클러스터를 제거
from sklearn.mixture import BayesianGaussianMixture
bgm = BayesianGaussianMixture(n_components=10, n_init=10, random_state=42)
bgm.fit(X)
np.round(bgm.weights_, 2)=> array([0.4 , 0.21, 0.4 , 0. , 0. , 0. , 0. , 0. , 0. , 0. ])
- 알고리즘이 자동으로 3개의 클러스터가 필요함을 감지
이 모델에서 클러스터 파라미터(가중치, 평균, 공분산 행렬 등)는 고정된 모델 파라미터가 아닌 클러스터 할당처럼 잠재 확률 변수로 취급됨
- z는 클러스터 파라미터와 클러스터 할당을 모두 포함함
베타 분포는 고정 범위 안에 놓인 값을 가진 확률 변수를 모델링할 때 자주 사용됨
- ※ 책 그림 9-22참고
- 이 경우 0~1의 범위
- SBP(stick-breaking process)
-
- φ=[0.3, 0.6, 0.5, ...] 를 가정하면 샘플의 30%가 클러스터 0에 할당되고 남은 샘플 60%가 클러스터 1에 할당됨
-
- 남은 샘플의 50%가 클러스터 2에 할당됨
-
이 프로세스는 새로운 샘플이 작은 클러스터보다 큰 클러스터에 합류할 가능성이 높은 데이터셋에 잘 맞는 모델
-
농도 α가 크면 φ값이 0에 가깝게 되고 SBP는 많은 클러스터를 만듦
-
반대로 농도가 낮으면 φ값이 1에 가깝게 되고 몇 개의 클러스터만 만들어짐
- 마지막으로 위샤트 분포를 사용해 공분산 행렬을 샘플링 함
-
파라미터 d와 V가 클러스터 분포 모양을 제어

잠재 변수 z에 대한 사전 지식이 사전 확률이라는 확률 분포 p(z)에 인코딩될 수 있음
- 예를 들어 클러스터가 적을 것이라는 사전 믿음(낮은 농도)를 가질 수 있음
- 반대로 풍부하다고 믿을 수 있음(높은 농도)
- 이런 클러스터 개수에 대한 사전 믿음은 weight_concentration_prior 매개변수로 조정 가능
- 데이터가 많을수록 사전 믿음은 중요하지 않음
- 위 그림처럼 큰 차이가 나는 그래프를 그리려면 사전 믿음이 매우 강하고 데이터는 적어야 함
베이즈 정리는 데이터 X를 관측하고 난 후 잠재 변수에 대한 확률 분포를 업데이트하는 방법을 설명
- X가 주어졌을 때 z의 조건부 확률인 사후 확률 분포 p(z|X)을 계산
p( z | X ) = 사후 확률 = (가능도 x 사전 확률) / 증거 = p( X | z )p( z ) / p( X )
베이즈 정리
- 가우시안 혼합 모델(그리고 많은 문제)에서 분모 p(X)는 계산하기 힘듦
-
가능한 모든 z값에 대해 적분해야 하기 때문(모든 클러스터 파라미터와 클러스터 할당의 조합을 고려해야 함)
-
이는 베이즈 통계학에 있는 주요 문제로, 해결하기 위한 방법으로 변분 추론을 사용할 수 있음
가우시안 혼합 모델은 타원형 클러스터에 잘 작동함
- 다른 모양을 가진 데이터셋에 훈련하면 나쁜 결과를 얻게 됨
- 반달 데이터셋을 군집하기 위해 베이즈 가우시안 혼합 모델을 사용한 결과

- 필사적으로 타원을 찾다보니, 2개가 아닌 8개의 클러스터를 찾은 모습
- 밀도 추정은 나쁘지 않으므로 이 모델은 이상치 감지를 위해 사용할 수 있을 것
9. 2. 4 이상치 탐지와 특이치 탐지를 위한 다른 알고리즘
임의의 모양을 가진 클러스터를 다룰 수 있는 군집 알고리즘들
- 사이킷런이 제공하는 이상치 탐지와 특이치 탐지 전용 알고리즘
이상치 탐지
PCA
-
보통 샘플의 재구성 오차와 이상치의 재구성 오차를 비교하면 일반적으로 후자가 훨씬 큼
-
매우 효과적인 이상치 탐지 기법
FAST-MCD
-
특히 데이터셋을 정제할 때 이상치 감지에 유용
-
보통 샘플(정상치)가 하나의 가우시안 분포에서 생성되었다고 가정(혼합된 것이 아니라)
-
이 가우시안 분포에서 생성되지 않는 이상치로 이 데이터셋이 오염되었다고 가정
-
알고리즘이 가우시안 분포의 파라미터를 추정할 때 이상치로 의심되는 샘플을 무시함
-
이런 기법으로 알고리즘이 타원형을 잘 추정하고 이상치를 잘 구분하도록 함
아이솔레이션 포레스트
-
고차원 데이터셋에서 이상치 감지를 위한 효율적인 알고리즘
-
무작위로 성장한 결정 트리로 구성된 랜덤 포레스트를 만듦
-
여기서 각 노드에서 특성을 랜덤하게 선택한 다음 랜덤한 임계값을 골라 데이터셋을 둘로 나눔
-
데이터셋은 점차 분리되어 모든 샘플이 다른 샘플과 격리될 때까지 진행
-
이상치를 일반적으로 다른 샘플과 멀리 떨어져 있으므로 정상 샘플과 적은 단계에서 격리
LOF
-
주어진 샘플 주위의 밀도와 이웃 주위의 밀도를 비교함
-
이상치는 k개의 최근접 이웃보다 더 격리될 수 있음
특이치 탐지
one-class SVM
-
커널 SVM 분류기는 모든 샘플을 고차원 공간에 매핑한 후 고차원 공간에서 선형 SVM 분류기를 사용해 두 클래스를 분리함
-
여기서는 샘플의 클래스가 하나이므로 대신 one-class SVM 알고리즘이 원본 공간으로부터 고차원 공간에 있는 샘플을 분리함
-
원본 공간에서는 모든 샘플을 둘러싼 작은 영역을 찾는 것에 해당
-
새로운 샘플이 이 영역안에 놓이지 않는다면 이는 이상치
-
-
조정할 하이퍼파라미터가 적음 (커널 SVM을 위한 하이퍼파라미터 하나와 마진 하이퍼파라미터)
-
마진은 실제 정상인 새로운 샘플을 실수로 이상치로 판단할 확률에 해당
-
-
고차원 데이터셋에서 잘 동작하지만, 대규모 데이터셋으로 확장은 어려움
'AI > Hands-on ML' 카테고리의 다른 글
| [핸즈온 머신러닝] 10장 - 케라스를 사용한 인공 신경망 2 (케라스로 딥러닝하기) (0) | 2021.03.06 |
|---|---|
| [핸즈온 머신러닝] 10장 - 케라스를 사용한 인공 신경망 1 (인공 신경망 소개) (0) | 2021.02.22 |
| [핸즈온 머신러닝] 9장 - 비지도 학습 1 (군집) (0) | 2021.01.30 |
| [핸즈온 머신러닝] 8장 - 차원 축소 (0) | 2021.01.24 |
| [핸즈온 머신러닝] 핸즈온 머신러닝2 정오표 (0) | 2021.01.22 |
