15. 순환 신경망 RNN
- 시계열 데이터를 분석해서 주식 가격 등을 예측하고, 자율 주행 시스템에서는 차의 이동 경로를 예측하여 사고를 피하도록 도움
- 일반적으로 이 신경망은 고정 길이 입력이 아닌 임의 길이를 가진 시퀀스를 다룰 수 있다. 문장, 문서, 오디오 샘플을 입력으로 받을 수 있고, 자연어 처리(NLP)에 매우 유용
15. 1 순환 뉴런과 순환 층
지금까지는 활성화 신호가 입력층에서 출력층 한 방향으로 흐르는 피드포워드 신경망 위주였지만, 순환 신경망은 뒤쪽으로 순환하는 연결도 있다는 차이점이 있음


- 입력을 받아 출력을 만들고, 자신에게도 출력을 보내는 뉴런 하나로 구성된 가장 간단한 RNN 구조
- 각 타임스텝 t(또는 프레임) 마다 이 순환 뉴런은 물론 x(t)와 이전 타임 스텝의 출력인 y(t-1)을 입력으로 받음
- 첫 번째 타임스텝에서는 이전 출력이 없으므로 일반적으로 0으로 설정
- 오른쪽처럼 시간에 따라 네트워크를 펼쳐 표현 가능(동일한 뉴런을 타임 스텝마다 하나씩 표현)

- 순환 뉴런으로 된 층
- 타임 스텝 t마다 모든 뉴런은 입력 벡터 x(t)와 이전 타임 스텝의 출력 벡터 y(t-1)을 받음 => 입력과 출력이 모두 벡터
- 각 순환 뉴런은 두 벌의 가중치를 가짐
- 하나는 입력 x(i)를 위한 것 -> 가중치 벡터 wx
- 하나는 이전 타임 스텝의 출력 y(t-1)을 위한 것 -> 가중치 벡터 wy
- 하나의 순환 뉴런이 아니라 순환 층 전체를 생각하면 가중치 벡터를 가중치 행렬 Wx와 Wy로 바꿀 수 있음
-> 순환 층 전체의 출력 벡터를 다음과 같이 계산 가능

- 피드포워드 신경망처럼 타임 스텝 t에서의 모든 입력을 행렬 X(t)로 만들어 미니배치 전체에 대해 순환 층의 출력을 한 번에 계산할 수 있음

15. 1. 1 메모리 셀
- 타임 스텝 t에서 순환 뉴런의 출력은 이전 타임 스텝의 모든 입력에 대한 함수이므로 일종의 메모리 형태라고 할 수 있음
- 타임 스텝에 걸쳐서 어떤 상태를 보존하는 신경망의 구성 요소를 메모리 셀(=셀) 이라고 함
- 하나의 순환 뉴런 또는 순환 뉴런의 층은 짧은 패턴만 학습할 수 있는 기본적인 셀

- 일반적으로 타임 스텝 t에서의 셀의 상태 h(t)는 그 타임 스텝의 입력과 이전 타입 스텝의 상태에 대한 함수
- h(t) = f(h(t-1), x(t))
- 타임 스텝 t에서의 출력 y(t)도 이전 상태와 현재 입력에 대한 함수
- 기본 셀의 경우 출력은 셀의 상태와 동일하지만, 위 그림처럼 더 복잡한 셀에서는 항상 그렇지는 않음
15. 1. 2 입력과 출력 시퀀스

시퀀스-투-시퀀스 네트워크
- RNN은 입력 시퀀스를 받아 출력 시퀀스를 만들 수 있음
- 주식가격 같은 시계열 데이터를 예측하는 데 유용
ex. 최근 N일치 주식가격을 주입하면 네트워크는 각 입력값보다 하루 앞선 가격을 출력해야 함
시퀀스-투-벡터 네트워크
- 입력 시퀀스를 네트워크에 주입하고, 마지막을 제외한 모든 출력을 무시할 수 있음
ex. 영화 리뷰에 있는 연속된 단어를 주입하면, 네트워크는 감성 점수를 출력함
벡터-투-시퀀스 네트워크
- 각 타임 스텝에서 하나의 입력 벡터를 반복해서 네트워크에 주입하고, 하나의 시퀀스를 출력할 수 있음
ex. 이미지(또는 CNN의 출력)를 입력하여 이미지에 대한 캡션을 출력할 수 있음
인코더-디코더
- 인코더라 부르는 시퀀스-투-벡터 네트워크 뒤에 디코더라 부르는 벡터-투-시퀀스 네트워크를 연결할 수 있음
ex. 한 언어의 문장을 다른 언어로 번역하는 데 사용 - 한 언어의 문장을 네트워크에 주입하면, 인코더는 이 문장을 하나의 벡터로 표현하고, 그 후 디코더가 이 벡터를 다른 언어의 문장으로 디코딩
- 인코더-디코더라 불리는 이중 단계 모델은 시퀀스-투-시퀀스가 RNN을 이용해 한 단어씩 번역하는 것보다 훨씬 더 잘 작동
- 문장의 마지막 단어가 번역의 첫 번째 단어에 영향을 줄 수 있기 때문
- 번역하기 전에 전체 문장이 주입될 때까지 기다릴 필요가 있음
15. 2 RNN 훈련하기
RNN을 훈련하는 방법은, 타임 스텝으로 네트워크를 펼치고 보통의 역전파를 사용하는 것
=> BPTT(backpropagation through time)

- 보통의 역전파와 같이, 첫 번째 정방향 패스가 펼쳐진 네트워크를 통과 (파선, 다섯개의 입력 시퀀스가 주입된 다섯 번의 타임 스텝)
- 비용함수 C(Y(0), Y(1), Y(2)) (T는 최대 타임 스텝)를 사용하여 출력 시퀀스가 평가됨
- 비용 함수의 그래디언트는 펼쳐진 네트워크를 따라 역방향으로 전파됨 (실선)
- 결국 모델 파라미터는 BPTT 동안 계산된 그래디언트를 사용해 업데이트됨
- 그래디언트가 마지막 출력 뿐만 아니라 비용 함수를 사용한 모든 출력에서 역방향으로 전파됨
(그림에서는 비용함수 계산시 Y(2),(3),(4) 를 사용했기 때문에 그래디언트는 이 세개의 출력을 거쳐 흐르지만 Y(0)과 Y(1)은 거치치 않음)
- 각 타임 스텝마다 같은 매개변수 W와 b가 사용되므로 역전파가 진행되면 모든 타임 스텝에 걸쳐 합산됨
15. 3 시계열 예측하기
웹사이트에서 시간당 접속 사용자의 수, 도시의 날짜별 온도, 여러 지표를 사용한 기업의 분기별 재정 안정성 등을 연구한다고 가정
- 모든 데이터는 타임 스텝마다 하나 이상의 값을 가진 시퀀스 -> 시계열
- 처음 두 예(접속 사용자수, 도시의 날짜별 온도)는 타임 스텝마다 하나의 값을 가지므로 단변량 시계열
- 재정 안정성 예시는 타임 스텝마다 여러 값(ex. 회사 수입, 부채 등)을 가지므로 다변량 시계열
- 예측 : 미래의 값을 예측하는 것
- 값 대체 : 과거 데이터에서 누락된 값 예측
시계열 생성
def generate_time_series(batch_size, n_steps):
freq1, freq2, offsets1, offsets2 = np.random.rand(4, batch_size, 1)
time = np.linspace(0, 1, n_steps)
series = 0.5 * np.sin((time - offsets1) * (freq1 * 10 + 10)) # wave 1
series += 0.2 * np.sin((time - offsets2) * (freq2 * 20 + 20)) # + wave 2
series += 0.1 * (np.random.rand(batch_size, n_steps) - 0.5) # + noise
return series[..., np.newaxis].astype(np.float32)- 요청한 만큼 n_steps 길이의 여러 시계열을 만드는 함수
- 각 시계열에는 타임 스텝마다 하나의 값만 있음(단변량)
- 이 함수는 [배치 크기, 타임 스텝 수, 1] 크기의 넘파이 배열을 반환
- 각 시계열은 진폭이 같고 진동 수와 위상이 랜덤한 두 개의 사인 곡선을 더하고 약간의 잡음을 추가
훈련 세트, 검증 세트, 테스트 세트 생성
n_steps = 50
series = generate_time_series(10000, n_steps + 1)
X_train, y_train = series[:7000, :n_steps], series[:7000, -1]
X_valid, y_valid = series[7000:9000, :n_steps], series[7000:9000, -1]
X_test, y_test = series[9000:, :n_steps], series[9000:, -1]- X_train은 7,000개의 시계열을 담음 ([7000, 50, 1] 크기)
- X_valid는 2,000개의 시계열을 담음
- X_test는 1,000개를 담음
-> 각 시계열마다 하나의 값을 예측해야 하기 때문에 타깃은 열 벡터 (y_train은 [7000, 1] 크기)
15. 3. 1 기준 성능
RNN을 시작하기전에, 기준 성능을 몇 개 준비하는 것이 좋음
- 가장 간단한 방법은 각 시계열의 마지막 값을 그대로 예측하는 순진한 예측
y_pred = X_valid[:, -1]
np.mean(keras.losses.mean_squared_error(y_valid, y_pred))=> 0.020211367
- 이 예제의 경우 평균 제곱 오차 0.020
- 또 다른 방법은 완전 연결 네트워크를 사용하는 것
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[50, 1]),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer="adam")
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
model.evaluate(X_valid, y_valid)=> 0.004145486224442721
- 이 네트워크는 입력마다 1차원 특성 배열을 기대하기 때문에 Flatten 층 추가
- 시계열 값의 선형 조합으로 예측하기 위해 선형 회귀 모델 사용
- MSE 손실, Adam 옵티마이저로 컴파일 후 20 epoch 동안 훈련 세트에서 훈련하여 검증 세트에서 평가 시 약 0.004의 MSE 결과로, 순진한 예측보다 나은 결과를 보여줌
15. 3. 2 간단한 RNN 구현하기
다음 코드는 가장 간단하게 만들 수 있는 RNN
model = keras.models.Sequential([
keras.layers.SimpleRNN(1, input_shape=[None, 1])
])- 하나의 뉴런으로 이루어진 하나의 층을 가짐
- 순환 신경망은 어떤 길이의 타임 스텝도 처리할 수 있기 때문에 입력 시퀀스의 길이를 지정할 필요가 없음 -> 첫 번째 입력 차원을 None으로 지정
- 이 모델을 훈련, 평가 하면 0.014에 달하는 MSE를 얻음
=> 순진한 예측보다 낫지만, 간단한 선형 모델을 앞지르지 못함
- 선형 모델은 각 뉴런에 대해 입력마다 하나의 파라미터를 가지고 편향이 있음(여기서 총 51개의 파라미터)
- 반면 기본 RNN의 순환 뉴런은 입력과 은닉 상태 차원마다 하나의 파라미터를 가지고 편향이 있음(기본 RNN에서는 총 3개의 파라미터)
15. 3. 3 심층 RNN
RNN은 셀을 여러 층으로 쌓는 것이 일반적 -> 심층 RNN
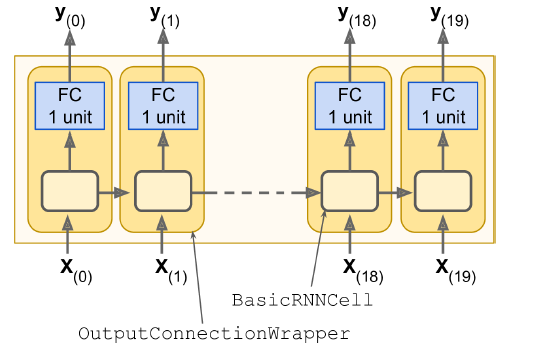
tf.keras로 심층 RNN을 구현하려면, 순환 층을 쌓으면 됨
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20, return_sequences=True),
keras.layers.SimpleRNN(1)
])- 모든 순환 층에서 return_sequences=True 설정 필요
- 마지막 출력만 관심 대상이면 마지막 층에서는 설정하지 않음
- 이 모델은 같은 조건으로 컴파일, 훈련, 평가 시 0.003의 MSE에 도달함
- 위 코드의 마지막 층을 변경할 수 있음
- 단변량 시계열을 예측하기 때문에 하나의 유닛이 필요하고 이는 타임 스텝마다 하나의 출력을 만들어야 한다는 뜻
- 하나의 유닛을 가진다는 것은 은닉 상태가 하나의 숫자라는 뜻
- 이 RNN은 한 타임 스텝에서 다음 타임 스텝으로 필요한 모든 정보를 나르기 위해 다른 순환 층의 은닉 상태를 주로 사용할 것
- 마지막 층의 은닉 상태는 필요하지 않음
- 또한 SimpleRNN은 기본적으로 tanh 활성화 함수를 사용하므로 예측된 값이 -1~1 사이 값을 가짐
=> 이런 이유로 출력층을 Dense로 바꾸는 경우가 많음
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20),
keras.layers.Dense(1)
])
- 두 번째 순환 층에서 return_sequences=True를 제거함(두 번째 순환 층이 마지막 층이 되었기 때문)
15. 3. 4 여러 타임 스텝 앞을 예측하기
지금까지처럼 다음 타임 스텝의 값만 예측하는게 아닌, 타깃을 적절히 바꾸어 여러 타임 스텝 앞의 값을 예측할 수 있음
ex. 1 스텝 앞이 아닌, 10 스텝 앞의 값으로 타깃을 바꾸어 10 스텝 앞 예측
-> 다음 값 10개를 예측하려면?
첫 번째 방법은 이미 훈련된 모델을 사용해 다음 값을 예측한 후, 이 값을 입력으로 추가하는 것
- 이 모델을 사용해 다시 다음 값을 예측하는 식
series = generate_time_series(1, n_steps + 10)
X_new, Y_new = series[:, :n_steps], series[:, n_steps:]
X = X_new
for step_ahead in range(10):
y_pred_one = model.predict(X[:, step_ahead:])[:, np.newaxis, :]
X = np.concatenate([X, y_pred_one], axis=1)
Y_pred = X[:, n_steps:]- 다음 스텝에 대한 예측은 보통 더 미래의 타임스텝에 대한 예측보다 정확함
(미래의 타임 스텝은 오차가 누적될 수 있기 때문)
- 이 모델은 한 번에 하나의 미래 스텝을 예측하기 위해 RNN을 사용하는 것보다 나음
두 번째 방법은 RNN을 훈련해 다음 값 10개를 한 번에 예측하는 것
- 시퀀스-투-벡터 모델을 사용하지만, 값 10개를 출력해야함 -> 타깃을 다음 10개의 값이 담긴 벡터로 바꿈
series = generate_time_series(10000, n_steps + 10)
X_train, Y_train = series[:7000, :n_steps], series[:7000, -10:, 0]
X_valid, Y_valid = series[7000:9000, :n_steps], series[7000:9000, -10:, 0]
X_test, Y_test = series[9000:, :n_steps], series[9000:, -10:, 0]- 1개의 유닛이 아니라 10개의 유닛을 가진 출력층 추가
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20),
keras.layers.Dense(10)
])- 모델 훈련시, 한 번에 다음 값 10개 예측 가능
Y_pred = model.predict(X_new)- 다음 10개 타임 스텝에 대한 MSE는 약 0.008으로, 잘 작동하는 모델
하지만 마지막 타임 스텝에서만 다음 값 10개를 예측하도록 모델을 훈련하는 대신 모든 타임 스텝에서 다음 값 10개를 예측하도록 모델을 훈련할 수 있음 => 시퀀스-투-시퀀스 RNN
- 마지막 타임 스텝에서의 출력뿐만 아니라 모든 타임 스텝에서 RNN 출력에 대한 항이 손실에 포함 됨
- 더 많은 오차 그래디언트가 모델로 흐르며, 시간에 따라 흐를 필요가 없음
- 훈련을 안정적으로 만들고 훈련 속도를 높임
타깃 시퀀스 준비
Y = np.empty((10000, n_steps, 10))
for step_ahead in range(1, 10 + 1):
Y[..., step_ahead - 1] = series[..., step_ahead:step_ahead + n_steps, 0]
Y_train = Y[:7000]
Y_valid = Y[7000:9000]
Y_test = Y[9000:]- 타임 스텝 0에서 모델이 타임 스텝 1에서 10까지 예측을 담은 벡터를 출력할 것
- 그 후, 타임 스텝 1에서는 타임 스텝 2에서 11까지 예측할 것
- 각 타깃은 입력 시퀀스와 동일한 길이의 시퀀스 (이 시퀀스는 타임 스텝마다 10차원 벡터를 담고 있음)
개선된 모델
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])- 시퀀스-투-시퀀스 모델로 바꾸기 위해, 모든 순환 층에 return_sequences=True 로 지정
- 모든 타임 스텝에서 출력을 Dense 층에 적용 => TimeDistributed 층 사용
- 이 층은 다른 층을 감싸 입력 시퀀스의 모든 타임 스텝에 이를 적용
- 각 타임 스텝을 별개의 샘플처럼 다루도록 입력의 크기를 바꾸어 효과적으로 수행
- 그 후 Dense층에 적용
- 마지막으로 출력 크기를 시퀀스로 되돌림
- 여기서 Dense 층이 유닛을 10개 가지므로 출력 차원의 길이는 10
MSE만을 계산하는 사용자 정의 지표 사용
def last_time_step_mse(Y_true, Y_pred):
return keras.metrics.mean_squared_error(Y_true[:, -1], Y_pred[:, -1])
optimizer=keras.optimizers.Adam(lr=0.01)
model.compile(loss="mse", metrics=[last_time_step_mse])- 훈련하는 동안은 모든 출력이 필요하지만, 예측/평가에는 마지막 타임 스텝의 출력만 사용 됨
- 평가를 위해 마지막 타임 스텝의 출력에 대한 MSE만을 계산하는 사용자 정의 지표 사용
- 검증 MSE로 0.006가 나옴 -> 이전 모델보다 25% 향상
- 이 RNN을 사용해 다음 값 10개를 예측하고, 이 값을 입력 시계열에 연결하고, 모델을 다시 사용해 다음 값 10개를 예측하는 방식을 반복할 수 있음 (어떤 길이의 시퀀스도 생성 가능) -> 16장에서 볼 새로운 음악이나 텍스트를 생성할 때 사용 가능
'AI > Hands-on ML' 카테고리의 다른 글
| [핸즈온 머신러닝] 17장(2) - 합성곱 오토인코더, 순환 오토인코더, 잡음 제거 오토인코더, 희소 오토인코더 (0) | 2021.05.12 |
|---|---|
| [핸즈온 머신러닝] 15장(2) - RNN과 CNN을 사용해 시퀀스 처리하기 (긴 시퀀스) (0) | 2021.04.27 |
| [핸즈온 머신러닝] 14장(4) - CNN을 통한 위치 추정, 객체 탐지, 시맨틱 분할 (1) | 2021.04.06 |
| [핸즈온 머신러닝] 14장(3) -케라스를 통한 CNN 구현 및 모델 사용 (0) | 2021.04.03 |
| [핸즈온 머신러닝] 14장(2) - CNN 구조 (LeNet-5, AlexNet, GoogLeNet, VGGNet, ResNet, Xception , SENet) (0) | 2021.04.01 |
