5. 서포트 벡터 머신(SVM)
- 매우 강력하고 선형이나 비선형 분류, 회귀, 이상치 탐색에도 사용할 수 있는 다목적 머신러닝 모델
- 복잡한 분류 문제에 잘 맞음
- 작거나 중간 크기의 데이터 셋에 적합
- 데이터를 선형으로 분리하는 최적의 선형 결정 경계를 찾는 알고리즘
5.1 선형 SVM 분류
- SVM 분류기는 클래스 사이에 가장 폭이 넓은 도로를 찾는 것과 같음
=> 라지 마진 분류라고 부름
- 여기서 마진은 두 데이터 군과 결정 경계가 떨어져 있는 정도를 의미
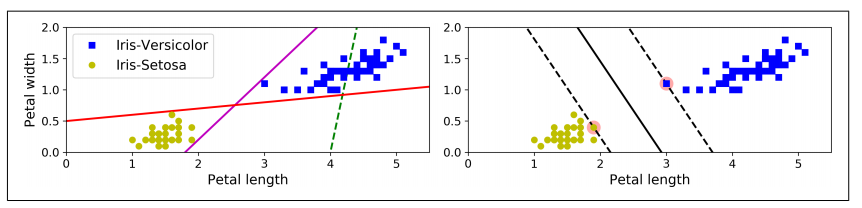
- 도로 바깥쪽에 훈련 샘플을 더 추가해도 결정 경계에는 영향을 미치지 않음(데이터가 추가 되더라도 안정적으로 분류해낼 수 있음)
- 도로 경계에 위치한 샘플에 의해 결정(의지)됨 => 이런 샘플을 서포트 벡터라고 함(오른쪽 그림의 동그라미)
- 서포트 벡터들은 두 클래스 사이의 경계에 위치한 데이터 포인트들
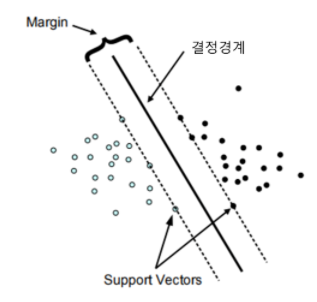
- 많은 데이터가 있지만 그 중 서포트 벡터들이 결정 경계를 만드는 데 영향을 줌
- 서포트 벡터들의 위치에 따라 결정 경계 위치도 달라짐
- 즉, 결정 경계는 이 서포트 벡터들에 의지함

- SVM은 특성의 스케일에 민감
- 왼쪽 그래프는 X1 스케일이 X0 스케일보다 훨씬 커서 가장 넓은 도로가 거의 수평에 가까움
- 오른쪽 그래프처럼 특성의 스케일을 조정하면(ex. 사이킷런의 StandardScaler 사용) 결정 경계가 훨씬 좋아짐
5.1.1 소프트 마진 분류
모든 샘플이 도로 바깥쪽에 올바르게 분류되어 있으면 하드 마진 분류라고 하는데, 하드 마진 분류에는 두 가지 문제점이 있음
- 데이터가 선형적으로 구분될 수 있어야 함
- 이상치에 민감함

이런 문제를 피하기위해 유연한 모델이 필요함
- 도로의 폭을 가능한 한 넓게 유지하는 것
- 마진 오류(샘플이 도로 중간이나 심지어 반대쪽에 있는 경우)사이에 적절한 균형을 잡아야함
=> 이를 소프트 마진 분류라고 함
소프트 마진 SVM은 하드 마진과 달리 C라는 하이퍼파라미터를 가짐

사이킷런의 SVM 모델을 만들 때 여러 하이퍼파라미터를 지정할 수 있는데, C는 그 중 하나
- C를 낮게 설정하면 왼쪽 그림과 같은 모델을 만듬
=> C, 즉 cost는 얼마나 많은 데이터 샘플이 다른 클래스에 놓이는 것을 허용하는지 결정
- 마진 오류는 나쁘므로 일반적으로 적은 것이 좋음
- 하지만 이 경우에는 왼쪽 모델이 마진 오류가 많지만 일반화가 더 잘 될 것
- C를 높게 설정하면 오른쪽과 같은 모델
- SVM 모델이 과대적합이라면 C를 감소시켜 모델을 규제할 수 있음
5.2 비선형 SVM 분류
선형적으로 분류할 수 없는 비선형 데이터셋을 다루는 방법은 4장에서처럼 다항 특성과 같은 특성을 더 추가하는 것
- 선형적으로 구분되는 데이터셋이 만들어짐

- 왼쪽 그래프는 하나의 특성 X1만을 가진 데이터셋 => 선형적으로 구분할 수 없음
- 오른쪽은 두번째 특성 X2=X1^2 을 추가하여 만들어진 2차원 데이터셋 => 선형적으로 구분 가능
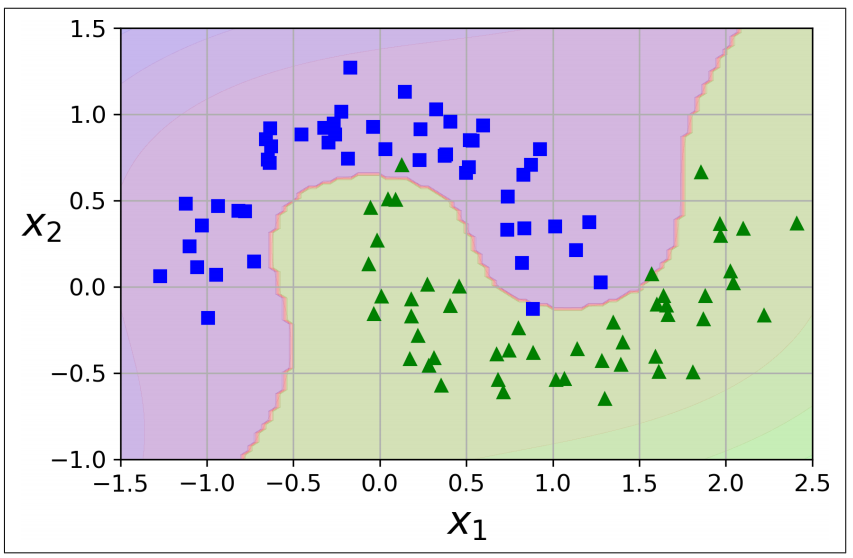
- 사이킷런의 make_moons 데이터셋과 PolynomialFeatrues변환기, LinearSVC 사용
5.2.1 다항식 커널
다항식 특성을 추가하는 것은 간단하고 (SVM뿐만 아니라) 모든 머신러닝 알고리즘에서 잘 작동함
- 하지만 낮은 차수의 다항식은 매우 복잡한 데이터셋을 잘 표현하지 못하고
- 높은 차수의 다항식은 굉장히 많은 특성을 추가하므로 모델을 느리게 만듦
SVM을 사용할 때 커널 트릭이라는 수학적 기교를 적용할 수 있음
- 커널 트릭은 실제로는 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있음
(즉, 주어진 데이터를 고차원 특성 공간으로 사상해주는 것)

- 실제로 특성을 추가하지 않기 때문에 엄청난 수의 특성 조합이 생기지 않음
※ 커널에는 Polynomial 커널, Sigmoid 커널, 가우시안 RBF 커널 등 종류가 많은데, 그 중 가우시안 RBF 커널이 성능이 좋아 자주 사용됨
- => 5.2.3 가우시안 RBF 절에서 설명

- SVC 클래스 사용
- 왼쪽은 3차 다항식 커널을 사용해 SVM 분류기를 훈련시킴
- 오른쪽은 10차 다항식 커널을 사용함
- 모델이 과대적합이라면 다항식 차수를 줄이고, 과소적합이면 늘려야함
- 매개변수 coef0는 모델이 높은 차수와 낲은 차수에 얼마나 영향을 받을지 조절(default=0)
5.2.2 유사도 특성
비선형 특성을 다루는 다른 기법은 각 샘플이 특정 랜드마크와 얼마나 닮았는지 측정하는 유사도 함수로 계산한 특성을 추가하는 것

- 예를 들어 앞에서 본 1차원 데이터셋에 두개의 랜드마크 x1=-2와 x2=1을 추가(위 왼쪽 그래프)
- y=0.3인 가우시안 방사 기저 함수(RBF)를 유사도 함수로 정의

- 이 함수의 값은 0(랜드마크에서 아주 멀리 떨어진 경우)부터 1(랜드마크와 같은 위치일 경우)까지 변화하며 종 모양으로 나타남
- x1이 -2에 가까울 수록 유사도가 1에 가까워짐
- x1=-1 샘플은 첫 번째 랜드마크에서 1만큼 떨어져있고 두 번재 랜드마크에서 2만큼 떨어져 있음
- 따라서 새로 만든 특성은 x2=exp(-0.3x1^2) 와 x3=exp(-0.3x2^2)
- 위 오른쪽 그래프는 변환된 데이터셋을 보여줌(원본 특성 제외) => 선형적으로 구분이 가능
랜드마크를 선택하는 방법
- 데이터셋에 있는 모든 샘플 위치에 랜드마크를 설정
- 차원이 매우 커지고 따라서 변환된 훈련 세트가 선형적으로 구분될 가능성이 높음
- 단점은 훈련 세트에 있는 n개의 특성을 가진 m개의 샘플이 m개의 특성을 가진 m개의 샘플로 변환되는 것
- 훈련 세트가 매우 클 경우 동일한 크기의 아주 많은 특성이 만들어짐
5.2.3 가우시안 RBF 커널
가우시안 RBF 커널은 다항 특성 방식과 마찬가지로 유사도 특성 방식도 머신러닝 알고리즘에 유용하게 사용됨
- 추가 특성을 모두 계산하려면 연산 비용이 많이 들어감(훈련 세트가 클 경우 특히 더)
- 여기서 커널 트릭을 이용하면 유사도 특성을 많이 추가하는 것과 같은 결과를 얻을 수 있음

- 커널에는 Polynomial 커널, Sigmoid 커널, 가우시안 RBF 커널 등 종류가 많은데, 그 중 가우시안 RBF 커널이 성능이 좋아 자주 사용됨
- 각 커널마다 최적화를 도와주는 매개변수들이 있으며, RBF 커널의 경우 gamma를 조정해야함
- gamma는 하나의 데이터 샘플이 영향력을 행사하는 거리를 결정
- gamma는 가우시안 함수의 표준편차와 관련되어 있는데, 클수록 작은 표준편차를 가짐
- SVM 기본 매개변수인 C도 있으므로 , 총 2개의 파라미터를 설정해야함
- (왼쪽 그래프) gamma를 증가시키면 종 모양 그래프가 좁아져서 각 샘플의 영향 범위가 작아짐
- 또한 결정 경계가 조금 더 불규칙해지고 각 샘플을 따라 구불구불하게 휘어짐
- 작은 gamma 값은 넓은 종 모양 그래프를 만들고 샘플이 넓은 범위에 걸쳐 영향을 주므로 결정 경계가 더 부드러워짐
- => 즉, 하이퍼파라미터 gamma(γ)가 규제의 역할을함
- 모델이 과대적합이면 감소시켜야하고, 과소적합이면 증가시켜야함
- 파라미터 C를 다시보면, C가 1000으로 큰 값일 때는 이상치를 인정하지 않으면서 분류함
- C와 gamma 모두 적정값을 찾아야함
- C는 데이터 샘플들이 다른 클래스에 놓이는 것을 허용하는 정도를 결정
- gamma는 결정 경계의 곡률을 결정
다른 커널도 있지만 거의 사용되지 않음
- 어떤 커널은 특정 데이터 구조에 특화되어 있음
- 문자열 커널이 가끔 텍스트 문서나 DNA 서열을 분류할 때 사용됨
- 여러가지 커널 중, 선형 커널을 먼저 시도해보는 것이 좋음
- (LinearSVC가 SVC(kernel="linear")보다 훨씬 빠름)
- 특히, 훈련세트가 아주 크거나 특성 수가 많은 경우에 좋음
- 훈련 세트가 너무 크지 않으면 가우시안 RBF 커널도 좋음(대부분 이 커널이 잘 맞음)
- 시간과 컴퓨팅 성능이 충분하다면 교차 검증과 그리드 탐색을 사용해 다른 커널도 시도해볼 수 있을 것
5.2.4 계산 복잡도

- LinearSVC 클래스는 선형 SVM을 위한 최적화된 알고리즘을 구현한 liblinear 라이브러리 기반
- 이 라이브러리는 커널 트릭을 지원하지 않지만 훈련 샘플과 특성 수에 거의 선형적으로 늘어남
- SVC는 커널 트릭 알고리즘을 구현한 libsvm 라이브러리를 기반
- 훈련 샘플 수가 커지면 엄청나게 느려짐
- 복잡하지만 작거나 중간규모의 훈련 세트에 잘 맞음
- 하지만 특성의 개수에는, 특히 희소 특성(각 샘플에 0이 아닌 특성이 몇개 없는 경우)의 경우 잘 확장됨
- 이 경우 알고리즘 성능이 샘플이 가진 0이 아닌 특성의 평균 수에 거의 비례
5.3 SVM 회귀
SVM 알고리즘은 다목적으로 사용할 수 있음
- 선형, 비선형 분류 뿐만 아니라 선형, 비선형 회귀에도 사용 가능
- SVM을 분류가 아닌 회귀에 적용하는 방법은 목표를 반대로 하는 것
- 일정한 마진 오류 안에서 두 클래스 간의 도로 폭이 가능한 한 최대가 되도록 하는 대신, SVM 회귀는 제한된 마진 오류(도로 밖의 샘플)안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 학습
- 도로의 폭은 하이퍼파라미터 ε으로 조절

- 무작위로 생성한 선형 데이터셋에 훈련시킨 두 개의 선형 SVM 회귀 모델을 보여줌
- 하나는 마진을 크게(ε=1.5), 다른 하나는 마진을 작게(ε=0.5)하여 만듦
- 마진 안에서는 훈련 샘플이 추가되어도 모델의 예측에는 영향이 없음
(모델 prediction은 굵은 선에 해당하는 선으로 예측)
=> 이 모델을 ε에 민감하지 않다(ε-insensitive)고 말함

- 비선형 회귀 작업을 처리하려면 커널 SVM 모델을 사용
- 위 그림은 임의의 2차방정식 형태의 훈련 세트에 2차 다항 커널을 사용한 SVM 회귀
- 왼쪽 그래프는 규제가 거의 없고(아주 큰 C), 오른쪽 그래프는 규제가 훨씬 많음(작은 C)
SVR은 SVC의 회귀 버전, LinearSVR은 LinearSVC의 회귀 버전
- LinearSVR은 (LinearSVC처럼) 필요한 시간이 훈련 세트의 크기에 비례해 선형적으로 늘어남
- SVR은 (SVC처럼) 훈련 세트가 커지면 훨씬 느려짐
5.4 SVM 이론
SVM의 예측은 어떻게 이루어지고, SVM의 훈련 알고리즘은 어떻게 동작하는 지에 대한 내용
- 편항을 b라고 하고, 특성의 가중치 벡터를 w라 표기
- 입력 특성에 편향을 위한 특성이 추가되지 않음
5.4.1 결정 함수와 예측
선형 SVM 분류기 모델은 단순히 결정함수 wT⋅x+b=w1x1+⋯+wnxn+bwT⋅x+b=w1x1+⋯+wnxn+b 를 계산해서 새로운 샘플 X의 클래스를 예측함
- 결과값이 0보다 크면 예측된 클래스는 양성 클래스(1), 아니면 음성 클래스(0)가 됨
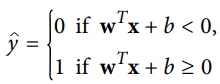

- 위 그래프를 보면 오른쪽에 있는 모델의 결정 함수가 나타나 있음
- 특성이 두 개(꽃잎 너비와 길이)인 데이터셋이기 때문에 2차원 평면임
- 결정 경계는 결정 함수의 값이 0인 점들로 이루어져 있음(두 평면의 교차점으로 직선, 굵은 실선)
- 점선은 결정 함수의 값이 1또는 -1인 점들
- 이 선분은 결정 경계에 나란하고 일정한 거리만큼 떨어져서 마진을 형성하고 있음
- 선형 SVM 분류기를 훈련한다는 것은 마진 오류를 하나도 발생하지 않거나 (하드 마진)
- 제한적인 마진 오류를 가지면서(소프트 마진) 가능한 한 마진을 크게 하는 w와 b를 찾는 것
5.4.2 목적 함수
- 결정 함수의 기울기는 가중치 벡터의 노름 ||w||와 같음
- 이 기울기를 2로 나누면 결정 함수의 값이 1 또는 -1이 되는 점들이 결정 경계로부터 2배 만큼 멀어짐
- 즉, 기울기를 2로 나누는 것은 마진에 2를 곱하는 것과 같음
- 가중치 벡터 w가 작을수록 마진은 커짐

마진을 크게 하기 위해 ||w||를 최소화하고자할 때
- 마진 오류를 하나도 만들지 않으려면(하드 마진)
- 결정 함수가 모든 양성 훈련 샘플에서는 1보다 커야하고
- 음성 훈련 샘플에서는 -1보다 작아야 함
- 아래와 같이 하드 마진 선형 SVM 분류기의 목적 함수를 제약이 있는 최적화 문제로 표현할 수 있음

소프트 마진 분류기의 목적 함수를 구성하려면 각 샘플에 대해 슬랙 변수를 도입해야 함
- 슬랙변수는 i번째 샘플이 얼마나 마진을 위반할지 정함
- 이 문제는 두 개의 상충되는 목표를 가짐
- 마진 오류를 최소화하기 위해 가능한 한 슬랙 변수의 값을 작게 만드는 것과
- 마진을 크게하기 위해 1/2wT⋅w를 가능한 작게 만드는 것
- 여기서 하이퍼파라미터 C는 두 목표 사이의 트레이드 오프를 정의함
- 아래 식에 있는 제약을 가진 최적화 문제가 됨

5.4.3 콰드라틱 프로그래밍
하드 마진과 소프트 마진 문제는 모두 선형적인 제약 조건이 있는 볼록 함수의 이차 최적화 문제이며,
이러한 문제를 콰드라틱 프로그래밍 이라고 함

다음과 같이 QP 파라미터를 지정하면 하드 마진을 갖는 선형 SVM분류기의 목적함수를 간단하게 검증할 수 있음
- np=n+1np=n+1, 여기서 nn은 특성 수.(+1+1은 편향 때문)
- nc=mnc=m, 여기서 mm은 훈련 샘플 수
- HH : np×npnp×np크기이고 왼쪽 맨 위의 원소가 00(편향 제외를 위해)인 것을 제외하고 단위행렬
- f=0f=0 : 모두 00으로 채워진 npnp차원의 벡터
- b=1b=1 : 모두 11로 채워진 ncnc차원의 벡터
- a(i)=−t(i)x˙(i)a(i)=−t(i)x˙(i), 여기서 x˙(i)x˙(i)는 편향을 위해 특성 x˙0=1x˙0=1을 추가한 x(i)x(i)와 같음
하드 마진 선형 SVM 분류기를 훈련시키는 한 가지 방법은 이미 준비되어 있는 QP 알고리즘에 관련 파라미터를 전달하는 것
- 결과 벡터 p는 편향 b=p0와 특성 가중치 wi=pi(여기서 i=1,2,3,,,n)을 담고 있음
- 비슷하게 소프트 마진 문제에서도 QP 알고리즘을 사용할 수 있음
커널 트릭을 사용하려면 제약이 있는 최적화 문제를 다른 형태로 바꾸어야함
5.4.4 쌍대 문제
원 문제 라는 제약이 있는 최적화 문제가 주어지면 쌍대 문제 라고 하는 관련된 다른 문제로 표현 가능
- 일반적으로 쌍대 문제 해는 원 문제 해의 하한값이지만,
- 어떤 조건하에서는 원 문제와 똑같은 해를 제공함
- SVM 문제는 이 조건을 만족시킴
=> 원 문제 또는 쌍대 문제 중 하나를 선택하여 풀 수 있음(둘 다 같은 해를 제공)

- 이식을 최소화하는 벡터 alpha hat을 찾았다면 아래 식을 사용해 원 문제의 식을 최소화하는 w hat과 b hat을 계산할 수 있음

- 훈련 샘플의 수가 특성 개수보다 작을 때 원 문제보다 쌍대 문제를 푸는 것이 빠름
- 또한 원 문제에서는 적용이 안되는 커널 트릭을 가능하게 함
- 다음 절에서 커널 트릭에 대한 설명이 포함됨
5.4.5 커널 SVM
2차원 데이터 셋에 2차 다항식 변환을 적용하고 선형 SVM 분류기를 변환된 이 훈련 세트에 적용한다고 가정
- 다음 식은 적용하고자 하는 2차 다항식 매핑 함수 ϕ

- 변환된 벡터는 2차원이 아닌 3차원
- 두 개의 2차원 벡터 a와 b에 2차 다항식 매핑을 적용한 다음 변환된 벡터로 점곱을 하면 다음과 같음
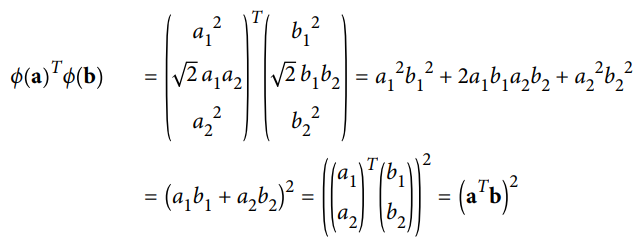
- 결과를 보면, 변환된 벡터의 점곱이 원래 벡터의 점곱의 제곱과 같음

- 모든 훈련 샘플에 변환 ϕ를 적용하면 쌍대 문제에 점곱 ϕ(x (i)) T ϕ(x (j)) 가 포함될 것
- 하지만 ϕ가 위 "2차 다항식 매핑"식에 정의된 2차 다항식 변환이라면 변환된 벡터의 점곱을 간단하게 (x (i)Tx (j))^2로 바꿀 수 있음 => 실제로 훈련 샘플을 변환할 필요가 없음
=> 식 "선형 SVM 목적 함수의 쌍대 형식" 에 있는 점곱을 제곱으로 바꾸면 됨
- 결과값은 실제로 훈련 샘플을 변환해 선형 SVM 알고리즘을 적용하는 것과 같으며, 계산량 측면에서 훨씬 효율적
=> 이것을 커널 트릭이라고 함
함수 K(a, b) = (a^T b)^2 을 2차 다항식 커널이라고 부름
- 머신러닝에서 커널은 변환 ϕ를 계산하지 않고(또는 ϕ를 모르더라도)
- 원래 벡터 a와 b에 기반하여 점곱 ϕ(a)^Tϕ(b)를 계산할 수 있는 함수
아래 식은 가장 널리 사용되는 커널의 일부

식 "쌍대 문제에서 구한 해로 원 문제 해 계산하기"는 선형 SVM 분류기일 경우 쌍대 문제를 풀어서 원 문제를 해결하는 방법을 알려줌
- 하지만 커널 트릭을 사용한다면 결국 예측 식에 ϕ(x^(i))를 포함해야함
- w hat의 차원이 매우 크거나 무한한 ϕ(x^(i))의 차원과 같아져야 하므로 이를 계산할 수 없음
- w hat을 모른 채로 예측을 만드려면
- 식 "쌍대 문제에서 구한 해로 원 문제 해 계산하기" 의 w hat에 대한 식을 새로운 샘플 x^(n)의 결정 함수에 적용해서 입력 벡터 간의 점곱으로만 된 식을 얻을 수 있음
- 이렇게 되면 커널 트릭을 사용할 수 있게 됨
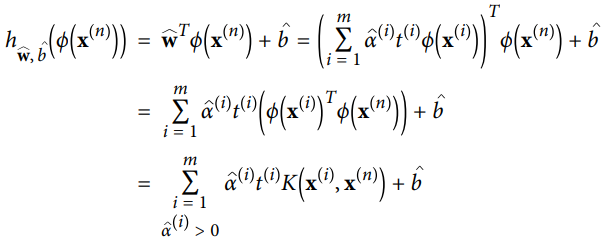
서포트 벡터만 α (i) ≠ 0이기 때문에 예측을 만드는 데는 전체 샘플이 아니라 서포트 벡터와 새 입력 벡터 x^(n)간의 점곱만 계산하면 됨
- 편한 b hat 도 커널 트릭을 사용해 계산해야 함

※ 머서의 정리
머서의 정리에 따르면 함수 K(a,b)가 머서의 조건(ex. K가 매개변수에 대해 연속, 대칭임. 즉 K(a,b)=K(b,a)등) 이라 부르는 몇 개 수학적 조건을 만족할 때 a와 b를 (더 높은 차원의) 다른 공간에 매핑하는 K(a,b)=ϕ(a)^Tϕ(b)와 같은 함수 ϕ가존재함
- ϕ를 모르더라도 ϕ가 존재하는 것은 알기 때문에 K를 커널로 사용할 수 있음
- 가우시안 RBF 커널의 경우 ϕ는 각 훈련 샘플을 무한 차원의 공간에 매핑하는 것으로 볼 수 있음(실제로 매핑X)
자주 사용하는 일부 커널(ex. 시그모이드 커널)은 머서의 조건을 모두 따르지 않지만 일반적으로 잘 작동함
5.4.6 온라인 SVM
온라인 SVM 분류기를 구현하는 한가지 방법은 원 문제로부터 유도된 다음 식의 비용함수를 최소화하기 위한 경사하강법을 사용하는 것(ex. SGDClassifier)
- 하지만 경사하강법은 QP 기반의 방법보다 훨씬 느리게 수렴

- 이 비용 함수의 첫번째 항은 모델이 작은 가중치 벡터 w를 가지도록 제약을 가해 마진을 크게 만듬
- 두번째 항은 모든 마진 오류를 계산
- 어떤 샘플이 도로에서 올바른 방향으로 벗어나 있다면 마진 오류는 0
- 그렇지 않다면 마진 오류는 올바른 방향의 도로 경계선까지의 거리에 비례
- 이 항을 최소화하면 마진 오류를 가능한 한 줄이고 크기도 작게 만듦
※ 힌지 손실
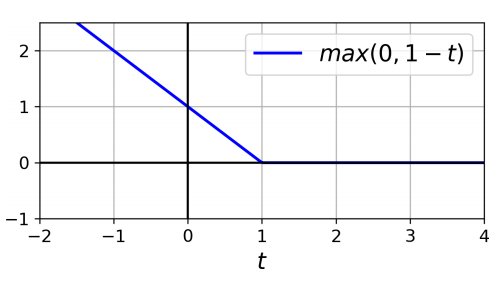
max(0,1-t) 함수를 힌지 손실 함수라고 함
- 이 함수는 t>=1 일때 0
- 이 함수의 도함수(기울기)는 t<1이면 -1이고 t>1이면 0
- t=1에서 미분 가능하지 않지만, 라쏘 회귀 처럼 t=1에서 서브그래디언트를 사용해 경사 하강법을 사용할 수 있음
(즉, -1과 0 사이의 값을 사용)
※ 참고
SVM의 기본 개념이 잘 정리되어 있음
'AI > Hands-on ML' 카테고리의 다른 글
| [핸즈온 머신러닝] 핸즈온 머신러닝2 정오표 (0) | 2021.01.22 |
|---|---|
| [핸즈온 머신러닝] 7장 - 앙상블 학습과 랜덤 포레스트 (0) | 2021.01.19 |
| [핸즈온 머신러닝] 6장 - 결정 트리 (0) | 2021.01.03 |
| [핸즈온 머신러닝] 4장 - 모델 훈련 (0) | 2020.12.08 |
| [핸즈온 머신러닝] 3장 - Classification (0) | 2020.11.23 |
