[핸즈온 머신러닝] 14장(1) - 합성곱 신경망을 사용한 컴퓨터 비전

14. 합성곱 신경망

 

합성곱 신경망 (CNN)

- 이미지 인식 분야에 사용되는 딥러닝 알고리즘

- 이미지 검색 서비스, 자율주행 자동차, 영상 자동 분류 시스템 등에 큰 기여

- 시각 분야 외에도 음성 인식, 자연어 처리(NLP) 같은 작업에도 사용

 

---

14. 1 시각 피질 구조

- 시각 피질 구조에 대한 연구 끝에, 시각 피질 안의 많은 뉴런이 작은 국부 수용장을 가진다는 것을 발견

- 뉴런들이 시야의 일부 범위 안에 있는 시각 자극에만 반응한다는 뜻

시각 피질의 국부 수용장은 수용장이라고 불리는 시야의 작은 영역에 있는 특정 패턴에 반응 / 시간 신호가 연속적인 뇌 모듈을 통과하면서 뉴런이 더 큰 수용장에 있는 더 복잡한 패턴에 반응함

- 뉴런 수용장들은 서로 겹칠 수 있으며, 합치며 전체 시야를 감싸게 됨

- 어떤 뉴런은 수평선의 이미지에만 반응하고, 다른 뉴런은 다른 각도의 선분에 반응하며

- 어떤 뉴런은 큰 수용장을 가져서 저수준 패턴이 조합된 더 복잡한 패턴에 반응함

=> 고수준 뉴런이 이웃한 저수준 뉴런의 출력에 기반하며, 이러한 구조로 전체 시야 영역의 복잡한 패턴을 감지할 수 있음

 

이런 연구를 기초로 지금의 합성곱 신경망이 나오게 되었음

- 1998년 얀 르쿤 등의 논문에서 손글씨 숫자를 인식하는 데 사용된 유명한 LeNet-5 구조가 소개됨

• 완전 연결층과 시그모이드 활성화 함수같은 요소 뿐만 아니라,
• 합성곱 층, 풀링 층이란 새로운 구성 요소도 소개됨

 

※ 이미지 인식 문제 - 완전 연결 층?

- 이미지 인식 문제에 일반적인 완전 연결 층의 심층 신경망을 사용할 경우, 큰 이미지에서는 아주 많은 파라미터가 만들어지기 때문에 문제가 됨

- 100*100 이미지는 픽셀 10000개로 이루어져 있고, 여기에 첫 번째 은닉층을 뉴런 1000개로 만들어도 연결이 총 천만 개가 생김 (심지어 첫 번째 은닉층일 뿐임)

=> CNN은 층을 부분적으로 연결하고 가중치를 공유하여 문제를 해결함

 

---

14. 2 합성곱 층

CNN의 가장 중요한 구성 요소인 합성곱 층

- 첫 번째 합성곱 층의 뉴런은 입력 이미지의 모든 픽셀에 연결되지 않고, 합성곱 층 뉴런의 수용장 안에 있는 픽셀에만 연결

- 두 번째 합성곱 층에 있는 각 뉴런은 첫 번째 층의 작은 사각 영역 안에 위치한 뉴런에 연결

사각 형태의 국부 수용장을 가진 CNN 층

- 이런 구조를 통해 네트워크가 첫 번째 은닉층에서는 작은 저수준 특성에 집중하고

- 그 다음 은닉층에서는 더 큰 고수준 특성으로 조합해나갈 수 있음

 

층과 제로 패딩 사이의 연결

패딩

- 합성곱 연산을 수행하기 전, 입력데이터 주변을 특정값으로 채워 늘리는 것

- CNN에서는 각 층이 2D로 표현되므로, 뉴런을 그에 상응하는 입력과 연결하기 더 쉬움

- 어떤 층의 i행, j열에 있는 한 뉴련은 이전 층 i에서 i+fh-1 까지의 행과 j에서 j+fw-1 까지의 열에 있는 뉴런의 출력에 연결됨 (fh = 수용장의 높이, fw = 수용장의 너비)

- 층의 높이와 너비를 이전 층과 같게 하기 위해 입력의 주위에 0을 추가하는 것이 일반적 => 제로 패딩

스트라이드 2를 사용해 차원 축소하기

 

스트라이드

- 입력데이터에 필터를 적용할 때, 필터가 이동할 간격 (한 수용장과 다음 수용장 사이의 간격)

- 수용장 사이에 간격을 두어 큰 입력층을 훨씬 작은 층에 연결할 수 있음 (모델의 계산 복잡도↓)

- 위 그림은 5*7 입력층(제로 패딩 적용)이 3*3 수용장과 스트라이드 2를 사용하여 3*4 층에 연결됨 

- 상위층의 i행, j열에 있는 뉴런이 이전 층의 i×sh 에서 i×sh+fh–1 까지의 행과, j×sw에서 j×sw+fw– 1 까지의 열에 위치한 뉴런과 연결됨 (sh = 스트라이드의 수직 값, sw = 스트라이드의 수평 값)

 

---

14. 2. 1 필터

뉴런의 가중치는 수용장 크기의 작은 이미지로 표현됨

두 개의 특성 맵을 만들기 위해 두 개의 다른 필터 적용하기

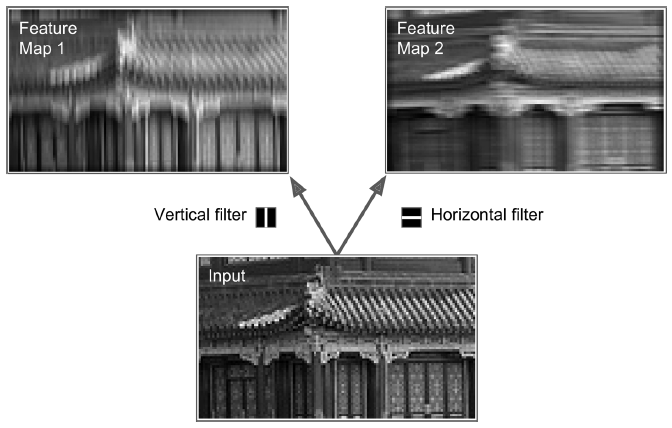
- 필터(합성곱 커널)라 부르는 두 개의 가중치 세트

- 첫 번째는 가운데 흰 수직선이 있는 검은 사각형(가운데 열은 1, 그 외는 모두 0인 7*7행렬)

• 이런 가중치의 뉴런은 가운데 수직선 제외 수용장의 모든 것을 무시함

- 두 번째 필터는 가운데 흰 수평선이 있는 검은 사각형

• 이 가중치를 사용한 뉴런은 가운데 수평선을 제외하고 모든 것을 무시함

- 그림의 입력 이미지를 네트워크에 주입하고, 한 층의 모든 뉴런에 같은 수직선 필터를 적용하면 왼쪽과 같이 이미지의 세로선에 해당하는 부분이 출력될 것이고

- 수평선 필터를 적용하면 오른쪽과 같이 이미지의 가로선에 해당하는 부분이 출력됨

=> 층의 전체 뉴런에 적용된 하나의 필터는 하나의 특성 맵을 만듦

- 여러 개의 필터를 사용해 이미지의 세부 특징을 추출해 학습을 진행

- CNN은 합성곱 층이 학습을 통해 자동으로 가장 유용한 필터를 찾고 상위 층은 이들을 연결해 더 복잡한 패턴을 학습함

 

---

14. 2. 2 여러 가지 특성 맵 쌓기

실제 합성곱 층은 여러가지 필터를 가지고 필터마다 하나의 특성 맵을 출력하므로, 합성곱 층의 출력을 3D로 표현하는 것이 더 정확

- 각 특성 맵의 픽셀은 하나의 뉴런에 해당

- 하나의 특성 맵 안에서는 모든 뉴런이 같은 파라미터(가중치, 편향)를 공유하지만, 다른 특성 맵의 뉴런은 다른 파라미터를 사용함

- 한 뉴런의 수용장은 이전 층에 있는 모든 특성 맵에 걸쳐 확장됨

=> 하나의 합성곱 층이 입력에 여러 필터를 동시에 적용해 입력의 여러 특성을 감지할 수 있음

 

여러가지 특성 맵으로 이루어진 합성곱 층과 세 개의 컬러 채널을 가진 이미지

- 입력 이미지는 컬러 채널마다 하나씩 여러 서브 층으로 구성될 수 있음

- 컬러 채널은 전형적으로 RGB 세 가지

- 합성곱 층 l에 있는 k 특성 맵의 i행, j열에 위치한 뉴런은 이전 l-1층에 있는 모든 특성 맵의 i×sh 에서 i×sh+fh–1 까지의 행과, j×sw에서 j×sw+fw– 1 까지의 열에 있는 뉴런의 출력에 연결됨

- 다른 특성 맵이더라도, 같은 i행과 j열에 있는 뉴런이라면 이전층에 있는 동일한 뉴런들의 출력에 연결됨

숫자 분류기를 위한 CNN 구조 / 출처: https://halfundecided.medium.com/%EB%94%A5%EB%9F%AC%EB%8B%9D-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-cnn-convolutional-neural-networks-%EC%89%BD%EA%B2%8C-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0-836869f88375

- 위 CNN 예시는 숫자 분류기를 위한 CNN sequence로, 앞 부분의 convolution layer를 참고

- 한 개의 28x28 이미지 입력값에 10개의 5x5 필터를 사용하여 24x24x10 matrix가 나오게 됨

- 이 결과값에 activation function(ex. ReLU)를 적용한 것이 첫 번째 convolution layer가 됨

 

 

합성곱 층에 있는 뉴런의 출력 계산

 

•  zi,j,k 는 합성곱 층(l층)의 k특성 맵에서 i행, j열에 위치한 뉴런의 출력
•  sh와 sw는 수직과 수평 스트라이드이고, fh와 fw는 수용장의 높이와 너비, fn'는 이전 층(l-1층)에 있는 특성 맵의 수
• xi',j',k' 는 l-1층의 i'행, j'열, k' 특성 맵(l-1 층이 입력층이면 k' 채널)에 있는 뉴런의 출력
• bk는(l층의) k특성 맵의 편향 - k특성 맵의 전체 밝기를 조정하는 다이얼로 생각
• wu,v,k',k는 l층의 k특성 맵에 있는 모든 뉴런과 (뉴런의 수용장에 연관된) u행, v열, 그리고 k'특성 맵에 위치한 입력 사이의 연결 가중치

 

합성곱 연산 예시

합성곱 연산(출처: 밑바닥부터 시작하는 딥러닝, https://excelsior-cjh.tistory.com/180)

- 합성곱 연산은 입력에 대한 가중치 합을 계산하고 편향을 더해줌

- 입력데이터와 필터 간 서로 대응되는 원소끼리 곱한 후 총합을 구하게됨

- 총합을 구한 후, 필터를 적용하고 편향을 더해줌

 

 

3차원 합성곱 연산 예시

3차원 input과 filter (출처: https://halfundecided.medium.com/%EB%94%A5%EB%9F%AC%EB%8B%9D-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-cnn-convolutional-neural-networks-%EC%89%BD%EA%B2%8C-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0-836869f88375)

3차원 데이터의 합성곱 (출처: 밑바닥부터 시작하는 딥러닝, https://excelsior-cjh.tistory.com/180)

- 3차원 합성곱 연산의 경우 입력 채널 수와 필터의 채널 수가 같아야 함

- 채널마다 입력 데이터 각 채널에 해당하는 가중치 필터로 합성곱 연산을 수행하여 총 합을 구함

 

---

14. 2. 3 텐서플로 구현

- 텐서플로에서 각 입력 이미지는 보통 [높이, 너비, 채널] 형태의 3D 텐서로 표현

- 하나의 미니배치는 [미니배치 크기, 높이, 너비, 채널] 형태의 4D 텐서로 표현

- 합성곱 층의 가중치는 [fh, fw, fn', fn] 형태의 4D 텐서로 표현

- 합성곱 층의 편향은 [fn] 형태의 1D 텐서로 나타냄

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.datasets import load_sample_image

# 샘플 이미지 로드
# 특성을 255로 나누어 0~1의 실수로 바꿈
china = load_sample_image("china.jpg") / 255
flower = load_sample_image("flower.jpg") / 255
images = np.array([china, flower])
batch_size, height, width, channels = images.shape

# 2개의 필터 생성
filters = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filters[:, 3, :, 0] = 1  # 수직선
filters[3, :, :, 1] = 1  # 수형선

# 필터를 두 이미지에 적용
# 스트라이드 1, 제로 패딩 적용
outputs = tf.nn.conv2d(images, filters, strides=1, padding="SAME")

# 첫 번째 이미지의 두 번째 특성맵 그리기
plt.imshow(outputs[0, :, :, 1], cmap="gray")
plt.axis("off") # Not shown in the book
plt.show()

=> 

첫 번째 특성맵

두 번째 특성맵

- tf.nn.conv2d()

• images: 입력의 미니배치(4D 텐서)
• filters: 적용될 일련의 필터(4D 텐서)
• strides: 1또는 4개의 원소를 갖는 1D 배열로 지정 가능 
  • 1D 배열의 가운데 두 개 원소는 수직/수평 stride(sk, sw) 이고, 첫 번째와 마지막 원소가 1이어야 함
  • 배치 스트라이드(일부 샘플 건너뛰기)와 채널 스트라이드(이전 층의 특성 맵이나 채널 건너뛰기)를 지정하는데 사용할 수 있음
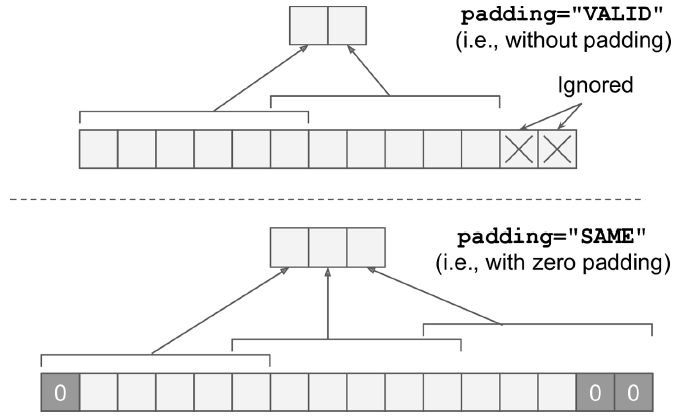
• padding: "VALID" 와 "SAME" 중 하나를 지정
  • VALID는 합성곱 층에 제로 패딩 사용X - 이미지 아래와 오른쪽 행과 열이 무시될 수 있음
  • SAME은 합성곱 층에 제로 패딩 사용 - 출력 크기는 입력 뉴런 수를 스트라이드로 나누어올림한 것과 같음
  • 입력 크기 13, 스트라이드 5 -> 출력크기 13/5=2.6 => 3 
  • 층의 출력이 입력과 동일한 공간 방향 차원을 가짐

 

padding= "VALID" 와 "SAME" (입력 너비13, 필터 너비 6, 스트라이드 5일 때)

 

 

실제  CNN은 보통 훈련 가능한 변수로 필터를 정의하여 신경망이 가장 잘맞는 필터를 학습할 수 있음

직접 변수를 만들지않고 keras.layers.Conv2D 층 사용

# 3*3 크기의 32개의 필터, 스트라이드 1, 제로 패딩을 사용하는 Conv2D 층
# 출력을 위해 ReLU 활성화 함수 적용
Conv = keras.layers.Conv2D(filters=32, kernel_size=3, strides=1,
                           padding="SAME", activation="relu")
                           
plot_image(crop(outputs[0, :, :, 0]))
plt.show()

=>

- 필터의 수, 높이, 너비 또는 스트라이드, 패딩 종류 등 많은 하이퍼파라미터 값을 찾아야 함

---

14. 2. 4 메모리 요구 사항

CNN은 합성곱 층이 많은 양의 RAM을 필요로 한다는 단점이 있음

- 훈련하는 동안에 역전파 알고리즘이 역방향 계산을 할 때 정방향에서 계산했던 모든 중간값을 필요로 함

• 5*5 필터로 스트라이드 1과 'SAME' 패딩을 이용해 150*100 크기의 특성 맵 200개를 만드는 합성곱 층
  • 입력이 150*100 RGB 이미지(채널 3개)면, 파라미터 수는 (5x5x3+1)x200 = 15,200개 (+1 : 편향)
  • 200개의 특성 맵마다 150*100개의 뉴런을 포함하고,
  • 각 뉴런은 5x5x3 = 75개의 입력에 대한 가중치 합을 계산해야 함
  • 즉 총 2억개 이상의 실수 곱셈이 발생함
  • 특성 맵이 32비트 부동소수로 표현된다면, 합성곱 층의 출력이 RAM의 200x150x100x32=9천6백만비트(12MB)를 점유할 것 -> 한 샘플에 대해서
  • 훈련 배치가 100개 샘플이면, 이 층은 1.2GB의 RAM을 사용할 것

- 메모리 부족으로 훈련 실패시

• 미니배치 크기를 줄이거나
• 스트라이드를 사용해 차원을 줄이거나 몇 개 층을 제거
• 32비트 부동소수 대신 16비트 부동소수 사용
• 여러 장치에 CNN을 분산시킴

 

---

14. 3 풀링 층

풀링 층의 목적은 계산량과 메모리 사용량, 파라미터 수를 줄이기 위해 입력 이미지의 부표본(즉, 축소본) 생성 => 결과값의 차원 축소

 

- 합성곱 층과 마찬가지로, 풀링 층의 각 뉴런은 이전 층의 작은 사각 영역의 수용장 안에 있는 뉴런의 출력과 연결되어 있음

- 크기, 스트라이드, 패딩 유형을 지정해야 하지만, 풀링 뉴런은 가중치가 없음

- 즉, 최대나 평균 같은 합산 함수로 입력값을 더하는 것이 전부 (max pooling, average pooling)

 

최대 풀링 층

 

최대 풀링 층(2x2 풀링 커널, 스트라이드 2, 패딩x)

- 각 수용장에서 가장 큰 입력값이 다음 층으로 전달되고, 나머지는 버려짐

- 스트라이드가 2이므로 출력 이미지의 높이와 너비는 입력 이미지의 절반이 됨

- 최대 풀링은 작은 변화에도 일정 수준의 불변성을 만듦

이동에 대한 불변성

• 위치만 이동시킨 같은 이미지 A, B, C
• 2x2 커널, 스트라이드 2인 최대 풀링층 통과
• 이미지 A와 B에서 최대 풀링층의 출력은 동일 -> 이동 불변성
• 이러한 불변성은 분류 작업처럼 예측이 이런 작은 부분에서 영향을 받지 않는 경우 유용함

- 최대 풀링은 매우 파괴적이라는 단점을 가짐

• 2x2 커널, 스트라이드 2를 사용하더라도 출력시 입력값의 75%를 잃게 됨
• 시맨틱 분할과 같이, 불변성이 아닌 등변성이 목표인 경우, 입력의 작은 변화도 출력에서 그에 상응하는 작은 변화로 이루어져야 함

숫자 분류기를 위한 CNN 구조 / 출처: https://halfundecided.medium.com/%EB%94%A5%EB%9F%AC%EB%8B%9D-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-cnn-convolutional-neural-networks-%EC%89%BD%EA%B2%8C-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0-836869f88375

- Convolution 과정을 통해 생성된 많은 결과값들에 pooling을 적용함 => 10개의 12x12 matrix

- correlation이 낮은 부분을 줄임으로써 결과값의 크기를 줄임

---

14. 3. 1 텐서플로 구현

최대 풀링 층 구현

# 2x2 커널 사용
# 스트라이드 default = 커널 크기 = 2
# 패딩 default = valid
max_pool = keras.layers.MaxPool2D(pool_size=2)

 

평균 풀링 층

MaxPool2D 대신 AvgPool2D 사용

- 최대값이 아닌 평균을 계산하는 것 제외 최대 풀링 층과 동일

- 최대 풀링 층이 일반적으로 성능이 더 좋음

- 평균을 계산하면 정보 손실이 적고,

- 최대 풀링은 가장 큰 특징만 유지함 -> 다음 층이 더 명확한 신호로 작업, 강력한 이동 불변성 제공, 연산 비용 덜 듦

 

깊이 방향 최대 풀링 층

- 공간 차원이 아닌, 깊이 차원으로 최대 풀링 및 평균 풀링 수행

- CNN이 다양한 특성에 대해 불변성을 학습할 수 있음

- EX. 동일 패턴이 회전된 여러 가지 필터를 학습했을 때, 회전에 상관없이 동일 출력을 만듦

- 비슷한 방법으로 두께, 밝기, 왜곡, 색상 등에 대한 불변성을 학습할 수 있음

 

- 텐서플로 저수준 딥러닝 API 사용

- 커널 크기와 스트라이드를 4개 원소를 가진 튜플로 지정

• 처음 세 값은 1 - 배치, 높이, 너비 차원을 따라 커널 크기와 스트라이드가 1
• 마지막 값 3 - 깊이 차원을 따라 커널 크기와 스트라이드를 3으로 지정

# 1x1x3 kernel & depth stride 3
output = tf.nn.max_pool(images,
                        ksize=(1, 1, 1, 3),
                        strides=(1, 1, 1, 3),
                        padding="valid")

Lambda 층으로 감싸 케라스 모델의 층으로 사용

depth_pool = keras.layers.Lambda(lambda X: tf.nn.max_pool(
    X, ksize=(1, 1, 1, 3), strides=(1, 1, 1, 3), padding="VALID"))

 

전역 평균 풀링 층

- 각 특성 맵의 평균을 계산 => 각 샘플의 특성 맵마다 하나의 숫자를 출력함

- 매우 파괴적인 연산이지만 출력층에는 유용

global_avg_pool = keras.layers.GlobalAvgPool2D()

- 아래 코드와 동일 (공간 방향을 따라 평균을 계산하는 lambda 층)

output_global_avg2 = keras.layers.Lambda(lambda X: tf.reduce_mean(X, axis=[1, 2]))

 

---

참고

velog.io/@dscwinterstudy/2020-01-28-1501-%EC%9E%91%EC%84%B1%EB%90%A8-8zk5xihhpz

excelsior-cjh.tistory.com/180

 

---

[AI/Hands-on ML] - [핸즈온 머신러닝] 14장(2) - CNN 구조 (LeNet-5, AlexNet, GoogLeNet, VGGNet, ResNet, Xception , SENet)

[핸즈온 머신러닝] 14장(2) - CNN 구조 (LeNet-5, AlexNet, GoogLeNet, VGGNet, ResNet, Xception , SENet)